题目内容
20.如图,在棱长为a的正方体ABCD-A1B1C1D1中.求:(1)面A1ABB1与面ABCD所成角的大小;
(2)二面角C1-BD-C的正切值.
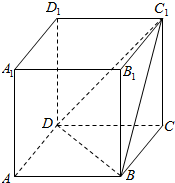
分析 (1)由面A1ABB1⊥面ABCD,能求出面A1ABB1与面ABCD所成角.
(2)取BD中点O,连结CO,C1O,由已知得∠COC1是二面角C1-BD-C的平面角,由此能求出二面角C1-BD-C的正切值.
解答  解:(1)∵AA1⊥平面ABCD,AA1?面A1ABB1,
解:(1)∵AA1⊥平面ABCD,AA1?面A1ABB1,
∴面A1ABB1⊥面ABCD,
∴面A1ABB1与面ABCD所成角为90°.
(2)取BD中点O,连结CO,C1O,
∵CD=CB=a,C1B=C1D=$\sqrt{2}a$,
∴CO⊥BD,C1O⊥BD,
∴∠COC1是二面角C1-BD-C的平面角,
∵$C{C}_{1}=a,CO=\frac{\sqrt{2}}{2}a$,
∴tan∠COC1=$\frac{C{C}_{1}}{OC}$=$\frac{a}{\frac{\sqrt{2}}{2}a}$=$\sqrt{2}$.
∴二面角C1-BD-C的正切值为$\sqrt{2}$.
点评 本题考查二面角的大小及其余弦值的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
8.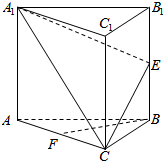 如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.
如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.
(1)求证:BF∥平面A1EC;
(2)求证:平面A1EC⊥平面ACC1A1.
(3)若各棱长相等,求二面角E-AC-B正切值.
 如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.
如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.(1)求证:BF∥平面A1EC;
(2)求证:平面A1EC⊥平面ACC1A1.
(3)若各棱长相等,求二面角E-AC-B正切值.
15.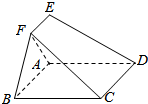 在如图所示的多面体ABCDEF中.四边形ABCD为矩形.EA⊥平面ABCD.EF∥AB,AB=4,AE=EF=2,则点D到平面FBC的距离为( )
在如图所示的多面体ABCDEF中.四边形ABCD为矩形.EA⊥平面ABCD.EF∥AB,AB=4,AE=EF=2,则点D到平面FBC的距离为( )
 在如图所示的多面体ABCDEF中.四边形ABCD为矩形.EA⊥平面ABCD.EF∥AB,AB=4,AE=EF=2,则点D到平面FBC的距离为( )
在如图所示的多面体ABCDEF中.四边形ABCD为矩形.EA⊥平面ABCD.EF∥AB,AB=4,AE=EF=2,则点D到平面FBC的距离为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 4 |
