题目内容
9．求证：$\sqrt{x-1}$-$\sqrt{x-2}$＜$\sqrt{x-3}$-$\sqrt{x-4}$（x≥4）分析 问题即证$\sqrt{x-1}$+$\sqrt{x-4}$＜$\sqrt{x-2}$+$\sqrt{x-3}$，两边平方、整理可知只需证$\sqrt{（x-1）（x-4）}$＜$\sqrt{（x-2）（x-3）}$，再次平方、整理后即证4＜6，显然成立．
解答 证明：∵x≥4，
∴x2-5x+4＜x2-5x+6，
∴（x-1）（x-4）＜（x-2）（x-3），
∴2$\sqrt{（x-1）（x-4）}$＜2$\sqrt{（x-2）（x-3）}$，
∴$（\sqrt{x-1}+\sqrt{x-4}）^{2}$＜$（\sqrt{x-2}+\sqrt{x-3}）^{2}$，
∴$\sqrt{x-1}$+$\sqrt{x-4}$＜$\sqrt{x-2}$+$\sqrt{x-3}$，
即$\sqrt{x-1}$-$\sqrt{x-2}$＜$\sqrt{x-3}$-$\sqrt{x-4}$．
点评 本题考查不等式的证明，对表达式的灵活变形是解决本题的关键，注意解题方法的积累，属于中档题．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
19．若a是实数，则“a2≠9”是“a≠3”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
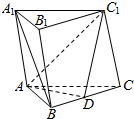如图，正三棱柱ABC-A1B1C1的各棱均相等，AB=2，D是BC上的一点，AD⊥C1D．
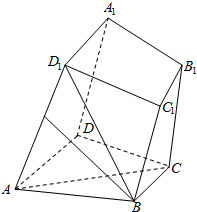如图所示，四棱柱ABCD-A1B1C1D1中，底面ABCD是梯形，AD∥BC，侧面ABB1A1为菱形，∠DAB=∠DAA1
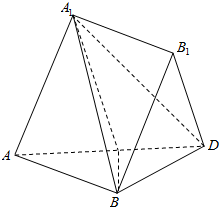如图，多面体A1B1-ABC中，△ABC与△AA1C都是边长为2的正三角形，四边形ABB1A1是平行四边形，且平面A1AC⊥平面ABC．
1．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0），F1，F2分别是它的左、右焦点，A是它的右顶点，过点F1作一条斜率为k的直线交双曲线于异于顶点的两点M、N，若∠MAN=90°，则该双曲线的离心率为（ ）
| A． | $\sqrt{3}$ | B． | 2 | C． | $\sqrt{5}$ | D． | $\frac{\sqrt{5}}{2}$ |