题目内容
15. 在如图所示的多面体ABCDEF中.四边形ABCD为矩形.EA⊥平面ABCD.EF∥AB,AB=4,AE=EF=2,则点D到平面FBC的距离为( )
在如图所示的多面体ABCDEF中.四边形ABCD为矩形.EA⊥平面ABCD.EF∥AB,AB=4,AE=EF=2,则点D到平面FBC的距离为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 4 |
分析 由题意,可将点D到平面BCF的距离可化为点A到平面BCF的距离,再转化为平面ABEF内点A到直线BF的距离,从而利用面积相等求解.
解答 解:∵四边形ABCD是矩形,
∴AD∥BC,
∴点D到平面BCF的距离可化为点A到平面BCF的距离,
又∵EA⊥平面ABCD,
∴平面ABEF⊥平面ABCD,
∴平面BCF⊥平面ABEF,
∴点A到平面BCF的距离可化为平面ABEF内点A到直线BF的距离,
则在平面ABEF内,BF=2$\sqrt{2}$,
∴$\frac{1}{2}$×2$\sqrt{2}$×h=$\frac{1}{2}$×4×2,
则h=2$\sqrt{2}$.
故选:B.
点评 本题考查线面、面面垂直,考查相似的转化能力,属于中档题.

练习册系列答案
相关题目
3.已知△ABC的内角∠A、∠B、∠C所对的边分别为a、b、c,且∠A=$\frac{π}{3}$,若a=1,则△ABC的周长l的取值范围是( )
| A. | (1,2) | B. | (1,3] | C. | (2,3] | D. | (1,3) |
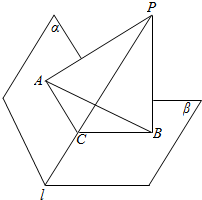
 如图所示,已知P是边长为a的菱形ABCD所在平面外一点,∠ABC=60°,PC⊥平面ABCD,PC=a,E为PA的中点.
如图所示,已知P是边长为a的菱形ABCD所在平面外一点,∠ABC=60°,PC⊥平面ABCD,PC=a,E为PA的中点.
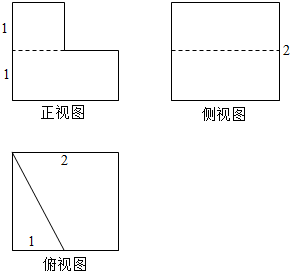
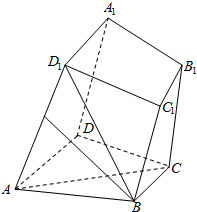 如图所示,四棱柱ABCD-A1B1C1D1中,底面ABCD是梯形,AD∥BC,侧面ABB1A1为菱形,∠DAB=∠DAA1
如图所示,四棱柱ABCD-A1B1C1D1中,底面ABCD是梯形,AD∥BC,侧面ABB1A1为菱形,∠DAB=∠DAA1