题目内容
5.用数学归纳法证明:1+2+22+…+2n-1=2n-1(n∈N*)分析 用数学归纳法证明:(1)当n=1时,去证明等式成立;(2)假设当n=k时,等时成立,用上归纳假设后,去证明当n=k+1时,等式也成立即可.
解答 证明:(1)当n=1时,左边=1,右边=21-1=1,
∴等式成立…2分
(2)假设当n=k时,等时成立,即1+2+22+…+2k-1=2k-1…4分
那么,当n=k+1时,1+2+22+…+2k-1+2k=2k-1+2k…6分
=2×2k-1
=2k+1-1…8分
这就是说,当n=k+1时,等式也成立…9分
根据(1)和(2),可知对n∈N*等式成立…10分
点评 本题考查数学归纳法,用好归纳假设是关键,考查逻辑推理与证明的能力,属于中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
16.实验测得五组(x,y)的值是(1,2),(2,3),(3,4),(4,4),(5,5),则y与x之间的回归直线的方程是( )
| A. | ∧y=x+1 | B. | ∧y=0.7x+1.5 | C. | ∧y=2 x+1 | D. | ∧y=x-1 |
10.在半径为8cm的圆中,5π3的圆心角所对的弧长( )
| A. | 400π3cm | B. | 20π3cm | C. | 200π3cm | D. | 40π3cm |
17.山东某市2008年至2012年新建商品住宅每平方米的均价y
(单位:千元)的数据如表:
(Ⅰ)求y关于x的线性回归方程ˆy=ˆb•x+ˆa;
(Ⅱ)利用(Ⅰ)中的回归方程,分析从2008年到2012年该市新建商品住宅每平方米均价的变化情况,并预测该市2015年新建商品住宅每平方米的均价.
附:回归直线的斜率和截距的最小二乘估计公式分别为ˆb=∑ni=1xiyi−nˉx•ˉy∑ni=1x2i−nˉx2,ˆa=ˉy−ˆb•ˉx.
(单位:千元)的数据如表:
| 年份 | 2008 | 2009 | 2010 | 2011 | 2012 |
| 年份序号x | 1 | 2 | 3 | 4 | 5 |
| 每平米均价y | 2.0 | 3.1 | 4.5 | 6.5 | 7.9 |
(Ⅱ)利用(Ⅰ)中的回归方程,分析从2008年到2012年该市新建商品住宅每平方米均价的变化情况,并预测该市2015年新建商品住宅每平方米的均价.
附:回归直线的斜率和截距的最小二乘估计公式分别为ˆb=∑ni=1xiyi−nˉx•ˉy∑ni=1x2i−nˉx2,ˆa=ˉy−ˆb•ˉx.
14.下列说法正确的是( )
| A. | f(x)=lnx2与g(x)=2lnx是同一个函数 | B. | cosπ12=√6−√24 | ||
| C. | △ABC中,cos(A+B)+sinC2的最小值是-1 | D. | 因为√2=2cosπ4,所以√2+√2=2cosπ8 |
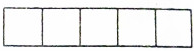 有一个经验级别达到25级的QQ好友,准备将自己QQ农场的15块空地连在一起的5块(如图)种上种植级别分别为22级、23级、25级的樱桃、荔枝和杨桃三种果树种子,如果同一种果树种子必须种在相邻的地中,则不同的种法有36种.
有一个经验级别达到25级的QQ好友,准备将自己QQ农场的15块空地连在一起的5块(如图)种上种植级别分别为22级、23级、25级的樱桃、荔枝和杨桃三种果树种子,如果同一种果树种子必须种在相邻的地中,则不同的种法有36种.