题目内容
14.将连续正整数1,2,…,n(n∈N*)从小到大排列构成一个数123…n,现从这个数中随机取一个数字,记P(n)为恰好取到0的概率,(如n=12时,此数为123456789101112,共15个数字,P(12)=$\frac{1}{15}$),则P(101)=$\frac{4}{65}$.分析 根据题意,首先分析n=101时,这个数的位数,进而可得其中0的个数,有等可能事件的概率公式,计算可得答案;
解答 解:F(n)为这个数的位数,
当100≤n≤999时,这个数有9个1位数组成,90个两位数组成,n-99个三位数组成,F(n)=3n-108,
所以,当n=101时,F(101)=3×101-108=195,即这个数中共有195个数字,
其中数字0的个数为12,
则恰好取到0的概率为P(101)=$\frac{12}{195}$=$\frac{4}{65}$,
故答案为:$\frac{4}{65}$.
点评 本题考查了古典概型的概率问题,关键是求出当n=101时,这个数中共有195个数字,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
4.R是△ABC三角形的外接圆半径,若ab<4R2cosAcosB,则∠C为( )
| A. | 锐角 | B. | 直角 | C. | 钝角 | D. | 无法判断 |
9.在花园小区内有一块三边长分别为6米、8米、10米的三角形绿化地,有一只小狗在其内部玩耍,若不考虑小狗的大小,则在任意指定的某时刻,小狗与三角形三个顶点的距离均超过2米的概率是( )
| A. | 1-$\frac{π}{24}$ | B. | 1$-\frac{π}{6}$ | C. | 1$-\frac{π}{12}$ | D. | 2$-\frac{π}{3}$ |
19.如图,在正方体ABCD-A1B1C1D1中,直线A1B与直线C1D1所成的角为( )
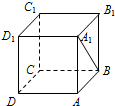

| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
6.已知函数f(x)=cos(2x+φ)(φ为常数)为奇函数,那么cosφ=( )
| A. | -$\frac{{\sqrt{2}}}{2}$ | B. | 0 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 1 |
4.某军区新兵50m步枪射击个人平均成绩x(单位:环)服从正态分布N(μ,o2),从这些个人平均成绩中随机抽取100个,得到如下频数分布表:
(Ⅰ)求μ和o2的值(用样本数学期望、方差代替总体数学期望、方差);
(Ⅱ)如果这个军区有新兵10000名,试估计这个军区新兵50m步枪射击个人平均成绩在区间(7.9,8.8]上的人数[参考数据:$\sqrt{0.8}$=0.9,若ξ:N(μ,o2),则P(μ-o-<ξ≤μ+o-)=0.6826,P(μ-2o-<ξ≤μ+2o-)=0.9544,P(μ-3o-<ξ≤μ+3o-=0.9974].
| x | 4 | 5 | 6 | 7 | 8 | 9 |
| 频数 | 1 | 2 | 26 | 40 | 29 | 2 |
(Ⅱ)如果这个军区有新兵10000名,试估计这个军区新兵50m步枪射击个人平均成绩在区间(7.9,8.8]上的人数[参考数据:$\sqrt{0.8}$=0.9,若ξ:N(μ,o2),则P(μ-o-<ξ≤μ+o-)=0.6826,P(μ-2o-<ξ≤μ+2o-)=0.9544,P(μ-3o-<ξ≤μ+3o-=0.9974].
 如图,在直角坐标系中,曲线段AB是函数y=1-x2图象的一部分,P为曲线段AB上异于点A,B一个动点,PM丄x轴,垂足为M,PN丄y轴,垂足为N.
如图,在直角坐标系中,曲线段AB是函数y=1-x2图象的一部分,P为曲线段AB上异于点A,B一个动点,PM丄x轴,垂足为M,PN丄y轴,垂足为N.