题目内容
20.$\frac{{x}^{2}}{a}$+$\frac{{y}^{2}}{b}$=1(a,b∈{1,2,3,4,…,100})的曲线中,所有圆面积的和等于5050π,离心率最小的椭圆方程为$\frac{{x}^{2}}{100}+\frac{{y}^{2}}{99}=1$或$\frac{{x}^{2}}{99}+\frac{{y}^{2}}{100}=1$.分析 由a=b可知圆的半径情况,代入圆的面积公式后由等差数列的前n项和得答案;再由$e=\frac{c}{a}=\sqrt{\frac{{c}^{2}}{{a}^{2}}}=\sqrt{\frac{{a}^{2}-{b}^{2}}{{a}^{2}}}=\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$可得,要使椭圆离心率最小,则$\frac{b}{a}$最大.
∴当a=100,b=99或a=99,b=100时椭圆离心率最小.由此求出椭圆的方程.
解答 解:由题意,所有圆的半径分别为:$\sqrt{1}、\sqrt{2}、\sqrt{3}、…、\sqrt{100}$,
则圆的面积分别为:π、2π、3π、…、100π,
则所有圆面积的和等于π(1+2+3+…+100)=5050π;
由$e=\frac{c}{a}=\sqrt{\frac{{c}^{2}}{{a}^{2}}}=\sqrt{\frac{{a}^{2}-{b}^{2}}{{a}^{2}}}=\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$,
∴要使椭圆离心率最小,则$\frac{b}{a}$最大.
∴当a=100,b=99或a=99,b=100时椭圆离心率最小.
∴离心率最小的椭圆方程为:$\frac{{x}^{2}}{100}+\frac{{y}^{2}}{99}=1$或$\frac{{x}^{2}}{99}+\frac{{y}^{2}}{100}=1$.
故答案为:5050π;$\frac{{x}^{2}}{100}+\frac{{y}^{2}}{99}=1$或$\frac{{x}^{2}}{99}+\frac{{y}^{2}}{100}=1$.
点评 本题考查圆的方程及面积,考查了椭圆的简单性质,训练了等差数列前n项和公式的应用,是中档题.

 名校课堂系列答案
名校课堂系列答案| A. | a>2$\sqrt{2}$ | B. | a$<2\sqrt{2}$ | C. | a<3 | D. | a>3 |
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $2\sqrt{3}$ |
| A. | 10 | B. | 12 | C. | 10π | D. | 12π |
| A. | f(x)的图象过点(0,$\frac{1}{2}$) | B. | f(x)在[$\frac{π}{12}$,$\frac{2π}{3}$]上是减函数 | ||
| C. | f(x)的一个对称中心是($\frac{5π}{12}$,0) | D. | f(x)的图象的一条对称轴是x=$\frac{5π}{12}$ |
| A. | c>b>a | B. | b>c>a | C. | a>b>c | D. | b>a>c |
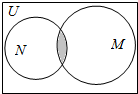 已知全集U=R,集合M={x|-1≤x≤3}和N={x|x=2k-1,k=1,2,…}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合的元素共有2个.
已知全集U=R,集合M={x|-1≤x≤3}和N={x|x=2k-1,k=1,2,…}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合的元素共有2个.