题目内容
(本题满分12分)已知椭圆C的中心在原点,对称轴为坐标轴,且过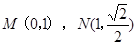
(Ⅰ)求椭圆C的方程,
(Ⅱ)直线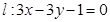 交椭圆C与A、B两点,求证:
交椭圆C与A、B两点,求证: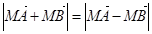
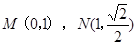
(Ⅰ)求椭圆C的方程,
(Ⅱ)直线
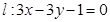 交椭圆C与A、B两点,求证:
交椭圆C与A、B两点,求证: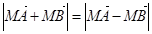

解:设椭圆C 的方程为

由椭圆C过点
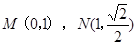 得:
得: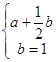
解得

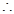 椭圆C的方程为
椭圆C的方程为
(Ⅱ)设
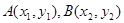 ,由
,由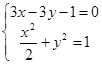
消去y整理得
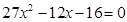 ,由韦达定理得,则
,由韦达定理得,则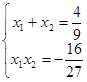
由
 两边平方整理可得
两边平方整理可得
只需证明

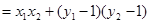
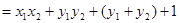
而
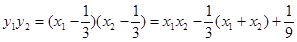

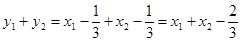
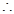

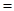

故
 恒成立
恒成立略

练习册系列答案
相关题目
题目内容
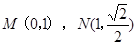
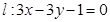 交椭圆C与A、B两点,求证:
交椭圆C与A、B两点,求证: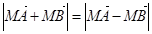


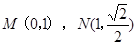 得:
得: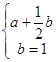

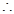 椭圆C的方程为
椭圆C的方程为
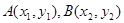 ,由
,由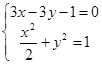
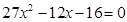 ,由韦达定理得,则
,由韦达定理得,则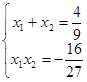
 两边平方整理可得
两边平方整理可得

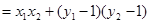
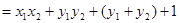
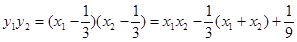

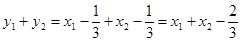
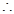

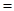

 恒成立
恒成立