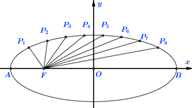
题目内容
(本题满分12分)设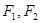 分别为椭圆C:
分别为椭圆C: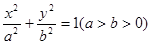 的左右两个焦点,椭圆上的点
的左右两个焦点,椭圆上的点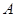 (
(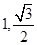 )到
)到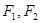 两点的距离之和等于4,设点
两点的距离之和等于4,设点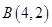 。
。
(1)求椭圆的方程;
(2)若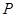 是椭圆上的动点,求线段
是椭圆上的动点,求线段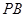 中点
中点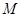 的轨迹方程;
的轨迹方程;
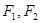 分别为椭圆C:
分别为椭圆C: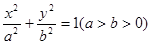 的左右两个焦点,椭圆上的点
的左右两个焦点,椭圆上的点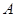 (
(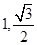 )到
)到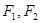 两点的距离之和等于4,设点
两点的距离之和等于4,设点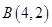 。
。(1)求椭圆的方程;
(2)若
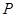 是椭圆上的动点,求线段
是椭圆上的动点,求线段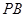 中点
中点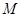 的轨迹方程;
的轨迹方程;解:(1) 依题意有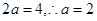 ,……(2分),
,……(2分),
又点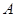 (
(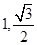 )在椭圆
)在椭圆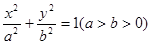 上,
上,
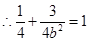 ,解得:
,解得: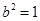 ,……(4分),
,……(4分),
故椭圆的方程为: ……(6分),
……(6分),
(2)设线段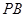 的中点为M(x,y) ,点P的坐标是(x0,y0),……(7分),
的中点为M(x,y) ,点P的坐标是(x0,y0),……(7分),
由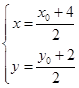 得
得  ……(9分),
……(9分),
由,点P在椭圆上,得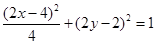 , ……(11分),
, ……(11分),
∴线段PA中点M的轨迹方程是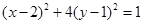 。……(12分),
。……(12分),
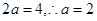 ,……(2分),
,……(2分),又点
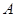 (
(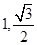 )在椭圆
)在椭圆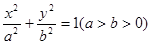 上,
上,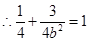 ,解得:
,解得: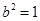 ,……(4分),
,……(4分),故椭圆的方程为:
 ……(6分),
……(6分),(2)设线段
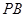 的中点为M(x,y) ,点P的坐标是(x0,y0),……(7分),
的中点为M(x,y) ,点P的坐标是(x0,y0),……(7分),由
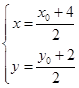 得
得  ……(9分),
……(9分),由,点P在椭圆上,得
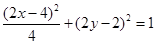 , ……(11分),
, ……(11分),∴线段PA中点M的轨迹方程是
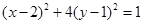 。……(12分),
。……(12分),略

练习册系列答案
相关题目
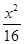 -
-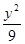 =1,椭圆的焦点恰好为双曲线的两个顶点,椭圆与双曲线的离心率互为倒数,则椭圆的方程为 .
=1,椭圆的焦点恰好为双曲线的两个顶点,椭圆与双曲线的离心率互为倒数,则椭圆的方程为 .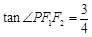 ,则椭圆的离心率为___________
,则椭圆的离心率为___________ 、
、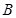 、
、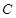 是椭圆
是椭圆 上的三个动点,若右焦点
上的三个动点,若右焦点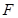 是
是 的重心,则
的重心,则
 的值是
的值是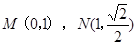
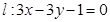 交椭圆C与A、B两点,求证:
交椭圆C与A、B两点,求证: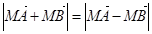
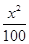 +
+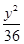 =1上一点,则DPF1F2的周长等于_________。
=1上一点,则DPF1F2的周长等于_________。 ,过椭圆的右焦点且与x轴垂直的直线与椭圆交于P、Q两点,椭圆的右准线与x轴交于点M,若
,过椭圆的右焦点且与x轴垂直的直线与椭圆交于P、Q两点,椭圆的右准线与x轴交于点M,若 为正三角形,则椭圆的离心率等于 ▲
为正三角形,则椭圆的离心率等于 ▲ 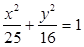 的长轴
的长轴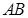 分成
分成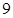 等分,过每个分点作
等分,过每个分点作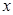 轴的垂线交椭圆的上半部分于
轴的垂线交椭圆的上半部分于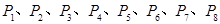 八个点,
八个点,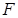 是椭圆的左焦点,则
是椭圆的左焦点,则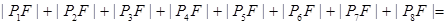 .
.