题目内容
如图,已知椭圆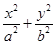
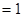 (a>b>0)的离心率
(a>b>0)的离心率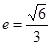 ,过顶点A、B的直线与原点的距离为
,过顶点A、B的直线与原点的距离为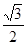 .
.
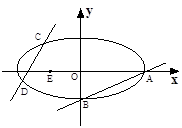
(1)求椭圆的方程.
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
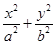
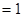 (a>b>0)的离心率
(a>b>0)的离心率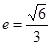 ,过顶点A、B的直线与原点的距离为
,过顶点A、B的直线与原点的距离为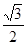 .
.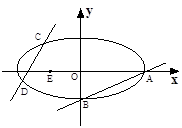
(1)求椭圆的方程.
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
(1)B(0,-b)和A(a,0)直线AB方程为:bx-ay-ab=0.
依题意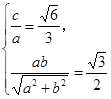 解得
解得 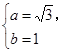


∴ 椭圆方程为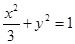 . --- 5分
. --- 5分
(2)假若存在这样的k值,由 得
得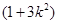
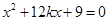 .
.
∴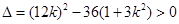 ①设
①设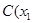 ,
, 、
、 ,
,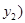 ,
,
则 ②
②
而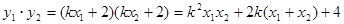 .
.
要使以CD为直径的圆过点E(-1,0),当且仅当CE⊥DE时,则 ,即
,即 ∴
∴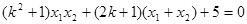 ③
③
将②式代入③整理解得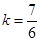 . --------------------------11分
. --------------------------11分
经验证,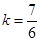 ,使①成立.
,使①成立. 

综上可知,存在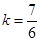 ,使得以CD为直径的圆过点E.
,使得以CD为直径的圆过点E.
依题意
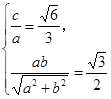 解得
解得 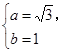


∴ 椭圆方程为
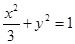 . --- 5分
. --- 5分(2)假若存在这样的k值,由
 得
得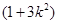
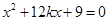 .
.∴
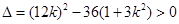 ①设
①设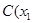 ,
, 、
、 ,
,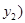 ,
,则
 ②
②而
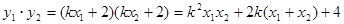 .
.要使以CD为直径的圆过点E(-1,0),当且仅当CE⊥DE时,则
 ,即
,即 ∴
∴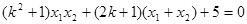 ③
③将②式代入③整理解得
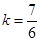 . --------------------------11分
. --------------------------11分经验证,
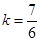 ,使①成立.
,使①成立. 

综上可知,存在
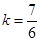 ,使得以CD为直径的圆过点E.
,使得以CD为直径的圆过点E.略

练习册系列答案
相关题目
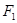 、
、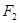 是椭圆
是椭圆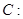
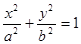 的左右焦点,
的左右焦点,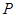 是
是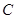 上一点,
上一点,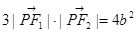 ,则
,则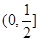
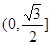
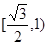
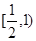
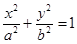 (a>b>0)的右焦点交椭圆于A.B两点,P为直线
(a>b>0)的右焦点交椭圆于A.B两点,P为直线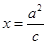 上任意一点,则∠APB为 ( )
上任意一点,则∠APB为 ( )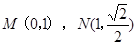
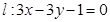 交椭圆C与A、B两点,求证:
交椭圆C与A、B两点,求证: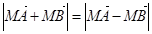
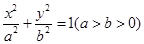 的一个焦点
的一个焦点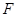 与抛物线
与抛物线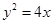 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为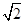 ,倾斜角为
,倾斜角为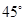 的直线
的直线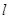 过点
过点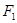 ,问抛物线
,问抛物线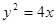 上是否存在一点
上是否存在一点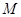 ,使得
,使得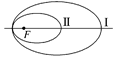
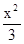 +
+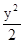 =1与椭圆
=1与椭圆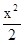 +
+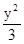 =l(l>0)有 ( )
=l(l>0)有 ( )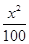 +
+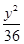 =1上一点,则DPF1F2的周长等于_________。
=1上一点,则DPF1F2的周长等于_________。