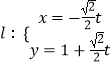题目内容
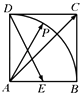
【题目】如图,四棱锥P﹣ABCD的底面ABCD是平行四边形,侧面PAD是边长为2的正三角形,AB=BD= ![]() ,PB=3.
,PB=3.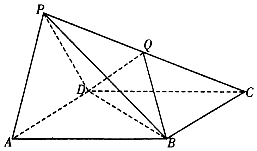
(1)求证:平面PAD⊥平面ABCD;
(2)设Q是棱PC上的点,当PA∥平面BDQ时,求二面角A﹣BD﹣Q的余弦值.
【答案】
(1)解:取AD中点O,连结OP,OB,
∵△PAD是边长为2的正三角形,∴OP= ![]() ,OP⊥AD,
,OP⊥AD,
又AB=AD= ![]() ,∴OB⊥AD,且OB=
,∴OB⊥AD,且OB= ![]() .
.
于是OB2+OP2=9=PB2,从而OP⊥OB.
所以OP⊥面ABCD,而OP面PAD,所以面PAD⊥面ABCD.
(2)连结AC交BD于E,则E为AC的中点,连结EQ,当PA∥面BDQ时,PA∥EQ,所以Q是BC中点.
由(1)知OA,OB,OP两两垂直,分别以OA,OB,OP所在直线为x,y,z轴建立空间直角坐标系,
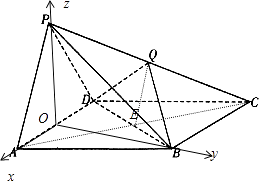
则B(0, ![]() ,0),C(﹣2,
,0),C(﹣2, ![]() ,0),D(﹣1,0,0),P(0,0,
,0),D(﹣1,0,0),P(0,0, ![]() ),Q(﹣1,
),Q(﹣1, ![]() ),
),
![]() ,
, ![]() .
.
设面BDQ的法向量为 ![]() ,由
,由 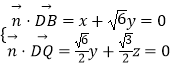 ,取
,取 ![]() .
.
面ABD的法向量是 ![]() ,∴cos<
,∴cos< ![]() >=﹣
>=﹣ ![]() .
.
∵二面角A﹣BD﹣Q是钝角,∴二面角A﹣BD﹣Q的余弦值为﹣ ![]() .
.
【解析】(1)取AD中点O,连结OP,OB,根据等边三角形三线合一可证OP⊥AD,由几何关系得出各线段长度后结合勾股定理证出OP⊥OB,由线面垂直得到面面垂直,(2)以O为坐标原点,以OA,OB,OP所在直线为x,y,z轴建立空间直角坐标系,由法向量得到二面角的余弦值.
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.

练习册系列答案
相关题目