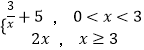题目内容
【题目】已知曲线C的参数方程为 
（φ为参数），以原点为极点，x轴的非负半轴为极轴建立极坐标系．
（Ⅰ）求曲线C的极坐标方程；
（Ⅱ）已知倾斜角为135°且过点P（1，2）的直线l与曲线C交于M，N两点，求 
的值．
【答案】解：（Ⅰ）曲线C的参数方程为 
（φ为参数），
消去参数得曲线C的普通方程为x2+（y﹣3）2=9，即x2+y2﹣6y=0，
即x2+y2=6y，即ρ2=6ρsinθ，故曲线C的极坐标方程为ρ=6sinθ．
（Ⅱ）设直线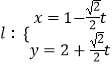 
（t为参数），将此参数方程代入x2+y2﹣6y=0中，
化简可得 
，显然△＞0；
设M，N所对应的参数分别为t1，t2，故 
，
∴ 
．
【解析】由三角函数中正、余弦平方和为1进行消参，得到平面直角坐标系方程，再改写成极坐标方程，（2）根据题意，写出直线l的参数方程，将参数方程代入曲线C的平面直角坐标方程，根据t的几何意义，可得值.
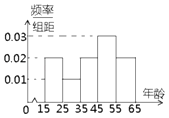
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题，拟定出台“延迟退休年龄政策”，为了了解人们对“延迟退休年龄政策”的态度，责成人社部进行调研，人社部从网上年龄在15～65岁的人群中随机调查100人，调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下：
年龄 | [15，25） | [25，35） | [35，45） | [45，55） | [55，65] |
支持“延迟退休”的人数 | 15 | 5 | 15 | 28 | 17 |
（1）由以上统计数据填2×2列联表，并判断是否95%的把握认为以45岁为界点的不同人群对“延迟退休年龄政策”的支持有差异；
45岁以下 | 45岁以上 | 总计 | |
支持 | |||
不支持 | |||
总计 |
（2）若以45岁为分界点，从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动，现从这8人中随机抽2人．
①抽到1人是45岁以下时，求抽到的另一人是45岁以上的概率；
②记抽到45岁以上的人数为X，求随机变量X的分布列及数学期望．
P（K2≥k0） | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
．
