题目内容
 已知函数f(x)=2sin(2x+
已知函数f(x)=2sin(2x+| π |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:直接利用五点法,令2x+
=0,
,π,
,2π,列表求出对应的x即可找到五个特殊点的坐标,即可得到函数图象.
| π |
| 3 |
| π |
| 2 |
| 3π |
| 2 |
解答:
解:(1)列表:
…(2分)
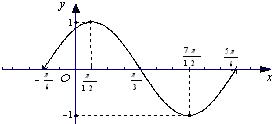 (2)描点,连线:得y=f(x)在一个周期内的图象.如右图所示.…(5分)
(2)描点,连线:得y=f(x)在一个周期内的图象.如右图所示.…(5分)
(描5个点正确给(1分),图象基本正确给2分)
| x | -
|
|
|
|
| ||||||||||
2x+
| 0 |
| π |
| 2π | ||||||||||
| f(x) | 0 | 1 | 0 | -1 | 0 |
 (2)描点,连线:得y=f(x)在一个周期内的图象.如右图所示.…(5分)
(2)描点,连线:得y=f(x)在一个周期内的图象.如右图所示.…(5分)(描5个点正确给(1分),图象基本正确给2分)
点评:本题考查三角函数作图,要注意取关键点和端点,注意自变量的取值范围,属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知正实数a,b满足a+2b=1,则
的最小值为( )
| b+a |
| ab |
A、3+2
| ||
B、1+
| ||
| C、4 | ||
D、2
|
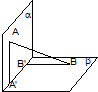 平面α⊥平面β,A∈α,B∈β,AB与两平面α、β所成的角分别为
平面α⊥平面β,A∈α,B∈β,AB与两平面α、β所成的角分别为 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则球的表面积是
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则球的表面积是