题目内容
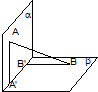平面α⊥平面β，A∈α，B∈β，AB与两平面α、β所成的角分别为| π |
| 4 |
| π |
| 6 |
考点：平面与平面垂直的性质
专题：空间位置关系与距离
分析：连接AB′，A′B，由已知中A'、B'分别为过A、B向两平面交线所作的垂线的垂足，故AB与两平面α、β所成的角分别为∠BAB′，∠ABA′，再由已知中AB=12，分别求出BB′，A′B的长，解三角形ABB′，即可求出A'B'的长．
解答：
解：连接AB′，A′B，如下图所示：
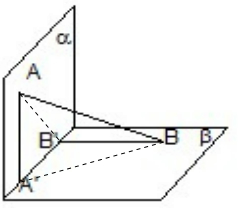
∵AB与两平面α、β所成的角分别为
和
即∠BAB′=
，∠ABA′=
，
又∵AB=12
∴BB′=6
，A′B=6
∴A′B′=
=6
故答案为：6．
∵AB与两平面α、β所成的角分别为
| π |
| 4 |
| π |
| 6 |
即∠BAB′=
| π |
| 4 |
| π |
| 6 |
又∵AB=12
∴BB′=6
| 2 |
| 3 |
∴A′B′=
| A′B2-BB′2 |
故答案为：6．
点评：本题考查的知识点是空间两点之间的距离，其中根据已知条件及线面夹角的定义，分别求出BB′，A′B的长，是解答本题的关键．
练习册系列答案
相关题目
已知A，B，C，D是函数y=sin（ωx+φ）一个周期内的图象上的四个点，如图所示，A（-| π |
| 6 |
| CD |
| π |
| 12 |
A、ω=
| ||||
B、ω=
| ||||
C、ω=2，φ=
| ||||
D、ω=2，φ=
|
已知函数f（x）=2sin（2x+