Question

【题目】已知椭圆(a＞b＞0)的一个焦点与抛物线y2＝4x的焦点F重合，且椭圆短轴的两个端点与点F构成正三角形.

(1)求椭圆的方程；

(2)若过点(1，0)的直线l与椭圆交于不同的两点P，Q，试问在x轴上是否存在定点E(m，0)，使恒为定值？若存在，求出E的坐标，并求出这个定值；若不存在，请说明理由.

Answer 1

【答案】（1）；（2）见解析.

【解析】试题分析：（1）求出抛物线的焦点坐标，可得c，再求出b的值，即可求椭圆的方程；
（2）分类讨论，设出直线方程，代入椭圆方程，利用韦达定理，结合向量的数量积公式，即可求得结论．

试题解析：

(1)由题意，知抛物线的焦点为F(，0)，

所以c＝＝.

因为椭圆短轴的两个端点与F构成正三角形，

所以b＝×＝1.

可求得a＝2，故椭圆的方程为＋y2＝1.

(2)假设存在满足条件的点E，当直线l的斜率存在时设其斜率为k，则l的方程为y＝k(x－1).

由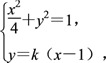

得(4k2＋1)x2－8k2x＋4k2－4＝0.

设P(x1，y1)，Q(x2，y2)，

所以x1＋x2＝，x1x2＝.

则＝(m－x1，－y1)，＝(m－x2，－y2)，

所以·＝(m－x1)(m－x2)＋y1y2

＝m2－m(x1＋x2)＋x1x2＋y1y2

＝m2－m(x1＋x2)＋x1x2＋k2(x1－1)(x2－1)

＝m2－＋＋k2

＝

＝

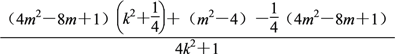
＝ (4m2－8m＋1)＋.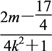

要使·为定值，则2m－＝0，

即m＝，此时·＝.

当直线l的斜率不存在时，

不妨取P，Q，

由E，可得＝，＝，

所以·＝－＝.

综上，存在点E，使·为定值.