题目内容
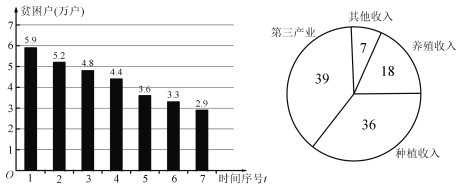
【题目】党的十八大以来,我国精准扶贫已经实施了六年,我国贫困人口从2012年的9899万人,减少到2018年的1660万人,2019年将努力实现减少贫困人口1000万人以上的目标,力争2020年在现行标准下,农村贫困人口全部脱贫,贫困县全部脱贫摘帽.某市为深入分析该市当前扶贫领域存在的突出问题,市扶贫办近三年来,每半年对贫困户(用![]() 表示,单位:万户)进行取样,统计结果如图所示,从2016年6月底到2019年6月底的共进行了七次统计,统计时间用序号
表示,单位:万户)进行取样,统计结果如图所示,从2016年6月底到2019年6月底的共进行了七次统计,统计时间用序号![]() 表示,例如:2016年12月底(时间序号为2)贫困户为5.2万户.
表示,例如:2016年12月底(时间序号为2)贫困户为5.2万户.
(1)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测到2020年12月底,该市能否实现贫困户全部脱贫;
,并预测到2020年12月底,该市能否实现贫困户全部脱贫;
(2)为尽快打赢脱贫攻坚战,该市扶贫办在2019年6月底时,对全市贫困户随机抽取了100户贫困户,对每个家庭最主要经济收入来源进行抽样调查,统计结果如图.并决定据此选派一批农业技术人员对全市所有贫困户中,家庭最主要经济收入来源为养殖收入和种植收入的贫困户进行对口帮扶,每一名农业技术人员对口帮扶贫困户90户,则该市应分别安排多少农业技术人员对家庭最主要经济收入来源为养殖收入和种植收入的贫困户进行对口帮扶?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
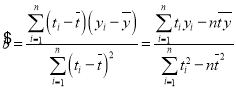 ,
,![]()
【答案】(1)![]() ,不能;(2)58人和116人.
,不能;(2)58人和116人.
【解析】
(1)由题意求得![]() 、
、![]() 后,代入公式即可得
后,代入公式即可得![]() 、
、![]() ,即可得线性回归方程;代入
,即可得线性回归方程;代入![]() 求得
求得![]() 即可得解;
即可得解;
(2)由统计图计算可得家庭最主要经济收入来源为养殖收入和种植收入的贫困户户数,即可得解.
(1)∵![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
2020年12月底时,![]() ,代入知
,代入知![]() ,不能实现贫困户全部脱贫.
,不能实现贫困户全部脱贫.
(2)2019年6月底时,贫困户共2.9万户,由图知,家庭最主要经济收入来源为养殖收入和种植收入分别占![]() 和
和![]() ,
,
![]() ,
,![]() ,
,
对家庭最主要经济收入来源为养殖收入和种植收入的贫困户分别安排58人和116人.

 阅读快车系列答案
阅读快车系列答案【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价 | 4 | 6 | 7 | 8 | 10 |
销量 | 60 | 50 | 45 | 30 | 20 |
(1) 请根据上表提供的数据画出散点图,并判断是正相关还是负相关;
(2) 求出![]() 关于
关于![]() 的回归直线方程,若单价为9元时,预测其销量为多少?
的回归直线方程,若单价为9元时,预测其销量为多少?
(参考公式:回归直线方程中公式 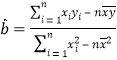 ,
,![]() )
)
【题目】下表数据为某地区某种农产品的年产量x(单位:吨)及对应销售价格y(单位:千元/吨) .
x | 1 | 2 | 3 | 4 | 5 |
y | 70 | 65 | 55 | 38 | 22 |
(1)若y与x有较强的线性相关关系,根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程.
(2)若该农产品每吨的成本为13.1千元,假设该农产品可全部卖出,利用上问所求的回归方程,预测当年产量为多少吨时,年利润Z最大?
(参考公式:回归直线方程为![]() ,
,![]() ,
,![]() )
)

