题目内容
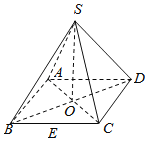
【题目】设m,n是两条不同直线,![]() ,
,![]() 是两个不同的平面,下列命题正确的是
是两个不同的平面,下列命题正确的是![]()
![]()
A.![]() ,
,![]() 且
且![]() ,则
,则![]()
B.![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]()
C.![]() ,
,![]() ,
,![]() ,则
,则![]()
D.![]() ,
,![]() 且
且![]() ,则
,则![]()
【答案】D
【解析】
对每一个命题逐一判断得解.
对于A,若m∥α,n∥β且α∥β,说明m、n是分别在平行平面内的直线,它们的位置关
系应该是平行或异面或相交,故A不正确;
对于B,若“mα,nα,m∥β,n∥β”,则“α∥β”也可能α∩β=l,所以B不成立.
对于C,根据面面垂直的性质,可知m⊥α,nβ,m⊥n,∴n∥α,∴α∥β也可能α∩β=l,
也可能α⊥β,故C不正确;
对于D,由m⊥α,n⊥β且α⊥β,则m与n一定不平行,否则有α∥β,与已知α⊥β矛盾,
通过平移使得m与n相交,且设m与n确定的平面为γ,则γ与α和β的交线所成的角即
为α与β所成的角,因为α⊥β,所以m与n所成的角为90°,故命题D正确.
故答案为D

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
【题目】为了更好地规划进货的数量,保证蔬菜的新鲜程度,某蔬菜商店从某一年的销售数据中,随机抽取了8组数据作为研究对象,如右下表所示(![]() (吨)为买进蔬菜的质量,
(吨)为买进蔬菜的质量,![]() (天)为销售天数):
(天)为销售天数):
(Ⅰ) 根据右表提供的数据在网格中绘制散点图,并判断![]() 与
与![]() 是否线性相关,若线性相关,用最小二乘法求出
是否线性相关,若线性相关,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]()

| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(Ⅱ)根据(Ⅰ)中的计算结果,若该蔬菜商店准备一次性买进蔬菜25吨,则预计需要销售多少天.
参考公式: ,
,![]()
【题目】某班共有学生45人,其中女生18人,现用分层抽样的方法,从男、女学生中各抽取若干学生进行演讲比赛,有关数据见下表(单位:人)
性别 | 学生人数 | 抽取人数 |
女生 | 18 |
|
男生 |
| 3 |
(1)求![]() 和
和![]() ;
;
(2)若从抽取的学生中再选2人做专题演讲,求这2人都是男生的概率.