题目内容
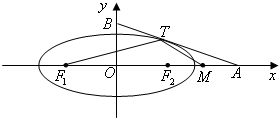
如图,椭圆
+
=1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=
.
(Ⅰ)求椭圆方程;
(Ⅱ)设F1、F2分别为椭圆的左、右焦点,M为线段AF1的中点,求证:∠ATM=∠AF1T.
| x2 |
| a2 |
| y2 |
| b |
| ||
| 2 |
(Ⅰ)求椭圆方程;
(Ⅱ)设F1、F2分别为椭圆的左、右焦点,M为线段AF1的中点,求证:∠ATM=∠AF1T.

(I)过点A、B的直线方程为
+y=1.
+
=1,
因为由题意得有惟一解,y=-
x+1
即(b2+
a2)x2-a2x2+a2-a2b2=0有惟一解,
所以△=a2b2(a2+4b2-4)=0(ab≠0),
故a2+4b2-4=0.
又因为e=
,即
=
,
所以a2=4b2.
从而得a2=2,b2=
,
故所求的椭圆方程为
+2y2=1.
(II)由(I)得c=
,
故F1(-
,0),F2(
,0),
从而M(1+
,0).
+2y2=1,
由y=-
x+1
解得x1=x2=1,
所以T(1,
).
因为tan∠AF1T=
-1,
又tan∠TAM=
,tan∠TMF2=
,
得tan∠ATM=
=
-1,
因此∠ATM=∠AF1T.
| x |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
因为由题意得有惟一解,y=-
| 1 |
| 2 |
即(b2+
| 1 |
| 4 |
所以△=a2b2(a2+4b2-4)=0(ab≠0),
故a2+4b2-4=0.
又因为e=
| ||
| 2 |
| a2-b2 |
| a2 |
| 3 |
| 4 |
所以a2=4b2.
从而得a2=2,b2=
| 1 |
| 2 |
故所求的椭圆方程为
| x2 |
| 2 |
(II)由(I)得c=
| ||
| 2 |
故F1(-
| ||
| 2 |
| ||
| 2 |
从而M(1+
| ||
| 4 |
| x2 |
| 2 |
由y=-
| 1 |
| 2 |
解得x1=x2=1,
所以T(1,
| 1 |
| 2 |
因为tan∠AF1T=
| ||
| 2 |
又tan∠TAM=
| 1 |
| 2 |
| 2 | ||
|
得tan∠ATM=
| ||||||
1+
|
| ||
| 2 |
因此∠ATM=∠AF1T.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目