题目内容

y轴上两定点B1（0，b）、B2（0，-b），x轴上两动点M，N．P为B1M与B2N的交点，点M，N的横坐标分别为XM、XN，且始终满足XMXN=a2（a＞b＞0且为常数），试求动点P的轨迹方程．
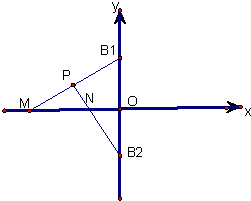
设P（x，y），M（xm，0），N（xn，0）（2分）
由M，P，B1三点共线，知
y-b
x-0
=
0-b
xm-0
（4分）
所以xm=
bx
b-y
（6分）
同理得xn=
bx
b+y
（9分）xm•xn=
b2x2
b2-y2
=a2（10分）
故点P轨迹方程为
x2
a2
+
y2
b2
=1（12分）
练习册系列答案
相关题目
已知椭圆C1的方程为
x2
4
+y2=1，双曲线C2的左、右焦点分别为C1的左、右顶点，而C2的左、右顶点分别是C1的左、右焦点．
（Ⅰ）求双曲线C2的方程；
（Ⅱ）若直线l：y=kx+
2
与椭圆C1及双曲线C2都恒有两个不同的交点，且l与C2的两个交点A和B满足
OA
•
OB
＜6（其中O为原点），求k的取值范围．
已知双曲线C：
x2
a2
-
y2
b2
=1(a＞0，b＞0)，直线l：y=
3
(x-4)关于直线l1：y=
b
a
x对称的直线l′与x轴平行．
（1）求双曲线的离心率；
（2）若点M（4，0）到双曲线上的点P的最小距离等于1，求双曲线的方程．
如图，椭圆
x2
a2
+
y2
b
=1（a＞b＞0）与过点A（2，0）B（0，1）的直线有且只有一个公共点T，且椭圆的离心率e=
3
2
．
（Ⅰ）求椭圆方程；
（Ⅱ）设F1、F2分别为椭圆的左、右焦点，M为线段AF1的中点，求证：∠ATM=∠AF1T．
如图，在以点O为圆心，AB为直径的半圆中，D为半圆弧的中心，P为半圆弧上一点，且AB=4，∠POB=30°，双曲线C以A，B为焦点且经过点P．
（1）建立适当的平面直角坐标系，求双曲线C的方程；
（2）设过点D的直线l与双曲线C相交于不同两点E、F，若△OEF的面积不小于2
2
，求直线l的斜率的取值范围．
如图，圆O的半径为定长r，A是圆O外一定点，P是圆上任意一点．线段AP的垂直平分线l和直线OP相交于点Q，当点P在圆上运动时，点Q的轨迹是（　　）
A．椭圆B．圆C．双曲线D．直线
已知双曲线的中心在原点O，其中一条准线方程为x=
3
2
，且与椭圆
x2
25
+
y2
13
=1有共同的焦点．
（1）求此双曲线的标准方程；
（2）（普通中学学生做）设直线L：y=kx+3与双曲线交于A、B两点，试问：是否存在实数k，使得以弦AB为直径的圆过点O？若存在，求出k的值，若不存在，请说明理由．
（重点中学学生做）设直线L：y=kx+3与双曲线交于A、B两点，C是直线L1：y=mx+6上任一点（A、B、C三点不共线）试问：是否存在实数k，使得△ABC是以AB为底边的等腰三角形？若存在，求出k的值，若不存在，请说明理由．
【理科】已知双曲线的中心在坐标原点O，一条准线方程为x=
3
2
，且与椭圆
x2
25
+
y2
13
=1有共同的焦点．
（1）求此双曲线的方程；
（2）设直线：y=kx+3与双曲线交于A、B两点，试问：是否存在实数k，使得以弦AB为直径的圆过点O？若存在，求出k的值，若不存在，请说明理由．
已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)上的点P到左右两焦点F1，F2的距离之和为2
2
，离心率为
2
2
．
（Ⅰ）求椭圆的方程；
（Ⅱ）过右焦点F2的直线l交椭圆于A、B两点，若y轴上一点M(0，
3
7
)满足|MA|=|MB|，求直线l的斜率k的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网