Question

【题目】已知点P到圆（x+2）2+y2=1的切线长与到y轴的距离之比为t（t＞0，t≠1）；

（1）求动点P的轨迹C的方程；

（2）当时，将轨迹C的图形沿着x轴向左移动1个单位，得到曲线G，过曲线G上一点Q作两条渐近线的垂线，垂足分别是P1和P2，求的值；

（3）设曲线C的两焦点为F1，F2，求t的取值范围，使得曲线C上不存在点Q，使∠F1QF2=θ（0＜θ＜π）.

Answer 1

【答案】（1）（1﹣t2）x2+y2+4x+3=0（2）（3）0＜t＜

【解析】

（1）设P（x，y），则P到圆的切线长为，利用勾股定理列方程化简即可得出动点P的轨迹C的方程；

（2）当t时，轨迹C的方程化为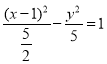：．可得曲线G的方程为．可得曲线G的渐近线方程为yx，yx．设Q（x0，y0），P1（m，m），P2（n，n），，．可得m，n．又y02＝2x02﹣5，利用数量积运算性质即可得出；

（3）对曲线C得类型进行讨论，得出∠F1QF2的最大值，利用三角恒等变换列不等式解出t的范围．

解：（1）圆（x+2）2+y2＝1的圆心为M（﹣2，0），半径r＝1，

设P（x，y），则P到圆的切线长为，

∴t|x|，

∴（x+2）2+y2﹣1＝t2x2，

整理得（1﹣t2）x2+y2+4x+3＝0．

则动点P的轨迹C的方程为：（1﹣t2）x2+y2+4x+3＝0．

（2）当t时，轨迹C的方程为﹣2x2+4x+3+y2＝0，即．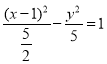

∴曲线G的方程为．

∴曲线G的渐近线方程为yx，yx．

设Q（x0，y0），P1（m，m），P2（n，n），

∴，．

∴m，n，

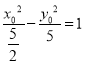∵，∴y02＝2x02﹣5，

∴（m﹣x0）（n﹣x0）+（m﹣y0）（n﹣y0）＝（m﹣x0）（n﹣x0）（x0﹣m）（x0﹣n）

（m﹣x0）（n﹣x0），

．

（3）曲线C的方程可化为（1﹣t2）（x）2+y23，

当0＜t＜1时，曲线C为焦点在x轴上的椭圆，椭圆标准方程为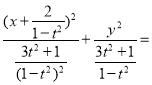1

∴当Q为短轴端点时，∠F1QF2取得最大值，设∠F1QF2的最大值为α，则tan2，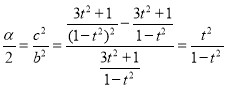

∴cosα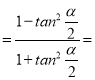1﹣2t2，

若曲线C上不存在点Q，使∠F1QF2＝θ，则θ＞α，

∴cosθ＜1﹣2t2，解得0＜t．

当t＞1时，曲线C为焦点在x轴的双曲线，∴0＜∠F1QF2≤π，

∴当0＜θ＜π时，曲线C上始终存在的Q使得∠F1QF2＝θ．

综上，当0＜t时，曲线C上不存在点Q，使∠F1QF2＝θ．