题目内容
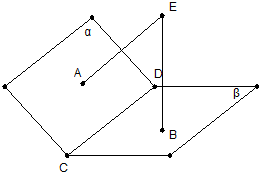
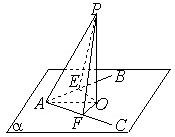
如图,已知∠BAC在平面α内,P∉α,∠PAB=∠PAC,求证:点P在平面α上的射影在∠BAC的平分线上.
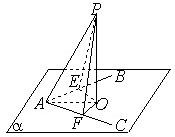

证明:作PO⊥α,PE⊥AB,PF⊥AC,
垂足分别为O,E,F,连接OE,OF,OA,
∵
⇒Rt△PAE≌Rt△PAF⇒AE=AF,
∵
⇒AB⊥PO,
又∵AB⊥PE,PO∩PE=P,
∴AB⊥平面PEO,
∴AB⊥OE,同理AC⊥OF.
在Rt△AOE和Rt△AOF,AE=AF,OA=OA,
∴Rt△AOE≌Rt△AOF,∴∠EAO=∠FAO,
即点P在平面α上的射影在∠BAC的平分线上.
垂足分别为O,E,F,连接OE,OF,OA,
∵
|
∵
|
又∵AB⊥PE,PO∩PE=P,
∴AB⊥平面PEO,
∴AB⊥OE,同理AC⊥OF.
在Rt△AOE和Rt△AOF,AE=AF,OA=OA,
∴Rt△AOE≌Rt△AOF,∴∠EAO=∠FAO,
即点P在平面α上的射影在∠BAC的平分线上.


练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目