题目内容
已知正六棱柱ABCDEF-A1B1C1D1E1F1的所有棱长均为2,G为AF的中点.
(1)求证:F1G∥平面BB1E1E;
(2)求证:平面F1AE⊥平面DEE1D1;
(3)求四面体EGFF1的体积.
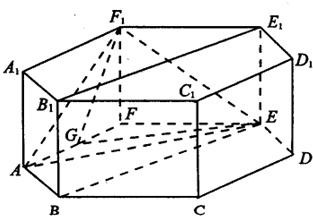
(1)求证:F1G∥平面BB1E1E;
(2)求证:平面F1AE⊥平面DEE1D1;
(3)求四面体EGFF1的体积.

(1)证明:因为AF∥BE,AF?平面BB1E1E,
所以AF∥平面BB1E1E,(2分)
同理可证,AA1∥平面BB1E1E,(3分)
所以,平面AA1F1F∥平面BB1E1E(4分)
又F1G?平面AA1F1F,所以F1G∥平面BB1E1E(5分)
(2)因为底面ABCDEF是正六边形,所以AE⊥ED,(7分)
又E1E⊥底面ABCDEF,所以E1E⊥AE,
因为E1E∩ED=E,所以AE⊥平面DD1E1E,(9分)
又AE?平面F1AE,所以平面F1AE⊥平面DEE1D1(10分)
(3)∵F1F⊥底面FGE,
VE-GFF1=VF1-GFE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目