题目内容
已知函数f(x)＝Asin(ωx＋φ)，x∈R(其中A＞0，ω＞0，0＜φ＜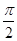
)的周期为π，且图象上一个最低点为M
.
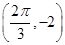(1)求f(x)的解析式；
(2)当x∈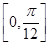
时，求f(x)的最值．
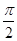)的周期为π，且图象上一个最低点为M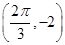.(1)求f(x)的解析式；
(2)当x∈
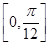时，求f(x)的最值．（1）f(x)＝2sin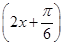
（2）最小值1，最大值
.
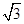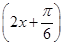（2）最小值1，最大值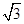.(1)由最低点为M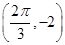，得A＝2.由T＝π，得ω＝
＝
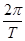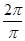＝2.
由点M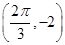在图象上得2sin
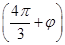＝－2，
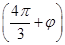即sin＝－1，∴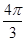
＋φ＝2kπ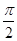－(k∈Z)，
即φ＝2kπ－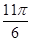
，k∈Z.又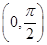φ∈
，∴φ＝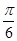
，∴f(x)＝2sin.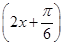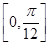
(2)∵x∈，∴2x＋∈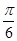
.
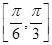∴当2x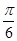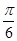＋＝，即x＝0时，f(x)取得最小值1；
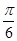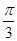当2x＋＝
，即x＝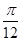
时，f(x)取得最大值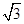
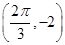，得A＝2.由T＝π，得ω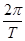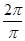＝＝＝2.由点M
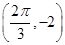在图象上得2sin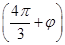＝－2，即sin
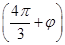＝－1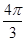，∴＋φ＝2kπ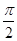－(k∈Z)，即φ＝2kπ－
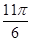，k∈Z.又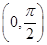φ∈，∴φ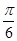＝，∴f(x)＝2sin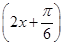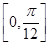.(2)∵x∈
，∴2x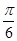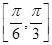＋∈.∴当2x＋
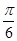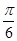＝，即x＝0时，f(x)取得最小值1；当2x＋
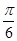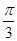＝，即x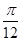＝时，f(x)取得最大值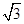
练习册系列答案
计算高手系列答案
相关题目
(x∈R)的图象，只需把函数y＝2sinx(x∈R)的图象上所有的点经过怎样的变换得到？
的部分图像如图所示.
的值；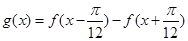
的单调递增区间.
（其中
，
，
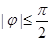）与坐标轴的三个交点
、
、
满足
，
，
为
的中点，
， 则
的值为____________
sinx，sinx)，b＝(cosx，sinx)，x∈
.
)＋
.
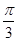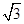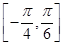上的最大值和最小值及取得最值时x的值．
.
＝－
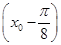，求f(x0)的值．
＋sin 
(ω＞0)的最小正周期为π，则( )
上单调递减
上单调递增
),使sinα+cosα=
;
|的最小正周期为π.