题目内容
给出如下五个结论:
①存在α∈(0,
),使sinα+cosα=
;
②存在区间(a,b),使y=cosx为减函数而sinx<0;
③y=tanx在其定义域内为增函数;
④y=cos2x+sin(-x)既有最大值和最小值,又是偶函数;
⑤y=sin|2x+
|的最小正周期为π.
其中正确结论的序号是 .
①存在α∈(0,
),使sinα+cosα=;②存在区间(a,b),使y=cosx为减函数而sinx<0;
③y=tanx在其定义域内为增函数;
④y=cos2x+sin(
-x)既有最大值和最小值,又是偶函数;⑤y=sin|2x+
|的最小正周期为π.其中正确结论的序号是 .
④
①中α∈(0,
)时,如图,由三角函数线知OM+MP>1,得sinα+cosα>1,故①错.
②由y=cosx的减区间为(2kπ,2kπ+π)(k∈Z),故sinx>0,因而②错.
③正切函数的单调区间是(kπ-,kπ+),k∈Z.
故y=tanx在定义域内不单调,故③错.
④y=cos2x+sin(-x)=cos2x+cosx
=2cos2x+cosx-1=2(cosx+
)2-
.
ymax=2,ymin=-.
故函数既有最大值和最小值,又是偶函数,故④正确.
⑤结合图象可知y=sin|2x+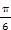
|不是周期函数,故⑤错.
)时,如图,由三角函数线知OM+MP>1,得sinα+cosα>1,故①错. ②由y=cosx的减区间为(2kπ,2kπ+π)(k∈Z),故sinx>0,因而②错.
③正切函数的单调区间是(kπ-
,kπ+),k∈Z.故y=tanx在定义域内不单调,故③错.
④y=cos2x+sin(
-x)=cos2x+cosx=2cos2x+cosx-1=2(cosx+
)2-.ymax=2,ymin=-
.故函数既有最大值和最小值,又是偶函数,故④正确.
⑤结合图象可知y=sin|2x+
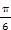|不是周期函数,故⑤错.
练习册系列答案
津桥教育计算小状元系列答案
相关题目
（
）的最小正周期为
．
的单调增区间；
个单位，再向上平移
个单位，得到函数
的图象．若
上至少含有
个零点，求
的最小值．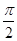
)的周期为π，且图象上一个最低点为M
.
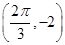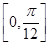时，求f(x)的最值．
，给出下列五个说法：
；②若
，则
；③
在区间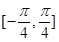
上单调递增；④函数
.⑤
成中心对称.
cos(3x-θ)-sin(3x-θ)是奇函数,则θ为( )
(k∈Z)
(k∈Z)
,
),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为( )
t+
)
t-
)
,
)的图象的一条对称轴方程是( )
在
上单调递减，则ω的取值范围是( )．
