题目内容
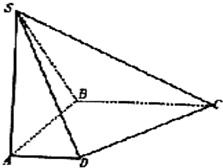
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,
SA=AB=BC=2a,AD=a.
(Ⅰ)求点C到平面SBD的距离;
(Ⅱ)求面SCD与面SBA所成的二面角的正切值.
分析:(I)根据已知中底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=2a,AD=a.我们根据VC-SBD=VS-BCD,求出三棱体积和△SBD的面积,即可得到点C到平面SBD的距离;
(Ⅱ)延长BA、CD相交于点E,连接SE,则SE是所求二面角的棱,∠BSC是面SCD与面SBA所成二面角的平面角,解三角形BSC,即可得到面SCD与面SBA所成的二面角的正切值.
解答: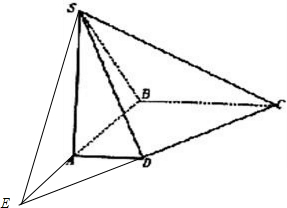
解:(Ⅰ)由题设条件得△SBD的面积是
S=BD•h=a•=a2设点C到平面SBD的距离为d由V
C-SBD=V
S-BCD得:
d==a所以点C到平面SBD的距离为
a(6分)
(Ⅱ)延长BA、CD相交于点E,连接SE,则SE是所求二面角的棱(7分)
∵AD∥BC,BC=2AD
∴EA=AB=SA∴SE⊥SB
∵SA⊥面ABCD得:面SEB⊥面EBC,EB是交线.
又BC⊥EB∴BC⊥面SEB故SB是SC在面SEB上的射影∴CS⊥SE,
∴∠BSC是面SCD与面SBA所成二面角的平面角(10分)
∵SB=
=2a,BC=2a,
又BC⊥SB∴
tan∠BSC===故所求二面角的正切值为
(12分)
点评:本题考查的知识点是二面角的平面角及求法,点到平面的距离计算,其中(1)的求解是所有的等体积法的理论基础是转化思想,而(2)的关键同样也是利用转化思想,求出二面角的平面角,将问题转化为解三角形问题.
练习册系列答案
相关题目
 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD, 解:(Ⅰ)由题设条件得△SBD的面积是S=
解:(Ⅰ)由题设条件得△SBD的面积是S= 解:(Ⅰ)由题设条件得△SBD的面积是S=
解:(Ⅰ)由题设条件得△SBD的面积是S=
 如图,在底面是直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,且
如图,在底面是直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,且 如图,在底面是直角梯形的四棱锥 P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4.AD=2,AB=
如图,在底面是直角梯形的四棱锥 P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4.AD=2,AB= (2012•宿州一模)如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.
(2012•宿州一模)如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.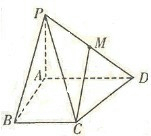 如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面 ABCD,PA=AB=BC=1,AD=2,M为PD中点.
如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面 ABCD,PA=AB=BC=1,AD=2,M为PD中点.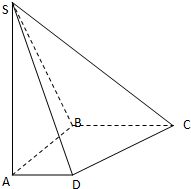 如图,在底面是直角梯形的四棱锥S-ABCD中,
如图,在底面是直角梯形的四棱锥S-ABCD中,