题目内容
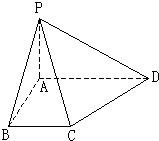 如图,在底面是直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,且∠ADC=arcsin
如图,在底面是直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,且∠ADC=arcsin
| ||
| 5 |
(I)求二面角P-CD-A的正切值;
(II)求点A到平面PBC的距离.
分析:(1)在底面ABCD内,过A作AE⊥CD,垂足为E,连接PE,易得∠PEA是二面角P-CD-A的平面角,在Rt△PAE中求出此角的正切值;
(2)在平面APB中,过A作AH⊥PB,垂足为H,可证得AH的长即为点A到平面PBC的距离,在等腰直角三角形PAB中解出AH即可.
(2)在平面APB中,过A作AH⊥PB,垂足为H,可证得AH的长即为点A到平面PBC的距离,在等腰直角三角形PAB中解出AH即可.
解答: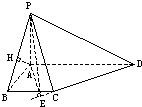 解:(1)在底面ABCD内,过A作AE⊥CD,垂足为E,连接PE,
解:(1)在底面ABCD内,过A作AE⊥CD,垂足为E,连接PE,
∵PA⊥平面ABCD,易证PE⊥CD,
∵∠PEA是二面角P-CD-A的平面角,
在Rt△AED中,AD=3a,∠ADE=arcsin
,
∴AE=AD•sin∠ADE=
a,
在Rt△PAE中,tan∠PEA=
=
,
∴二面角P-CD-A的正切值为
;
(II)在平面APB中,过A作AH⊥PB,垂足为H
∵PA⊥平面ABCD,
∴PA⊥BC,
又AB⊥BC,∴BC⊥平面PAB,
∴平面PBC⊥平面PAB,
∴AH⊥平面PBC,
故AH的长即为点A到平面PBC的距离,
在等腰直角三角形PAB中,AH=
a,
所以点A到平面PBC的距离为
a.
 解:(1)在底面ABCD内,过A作AE⊥CD,垂足为E,连接PE,
解:(1)在底面ABCD内,过A作AE⊥CD,垂足为E,连接PE,∵PA⊥平面ABCD,易证PE⊥CD,
∵∠PEA是二面角P-CD-A的平面角,
在Rt△AED中,AD=3a,∠ADE=arcsin
| ||
| 5 |
∴AE=AD•sin∠ADE=
3
| ||
| 5 |
在Rt△PAE中,tan∠PEA=
| PA |
| AE |
| ||
| 3 |
∴二面角P-CD-A的正切值为
| ||
| 3 |
(II)在平面APB中,过A作AH⊥PB,垂足为H
∵PA⊥平面ABCD,
∴PA⊥BC,
又AB⊥BC,∴BC⊥平面PAB,
∴平面PBC⊥平面PAB,
∴AH⊥平面PBC,
故AH的长即为点A到平面PBC的距离,
在等腰直角三角形PAB中,AH=
| ||
| 2 |
所以点A到平面PBC的距离为
| ||
| 2 |
点评:本题主要考查了平面与平面之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
相关题目
 如图,在底面是直角梯形的四棱锥 P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4.AD=2,AB=
如图,在底面是直角梯形的四棱锥 P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4.AD=2,AB= (2012•宿州一模)如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.
(2012•宿州一模)如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1. 如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面 ABCD,PA=AB=BC=1,AD=2,M为PD中点.
如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面 ABCD,PA=AB=BC=1,AD=2,M为PD中点. 如图,在底面是直角梯形的四棱锥S-ABCD中,
如图,在底面是直角梯形的四棱锥S-ABCD中,