题目内容
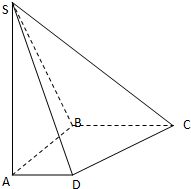 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=| 1 | 2 |
(1)求四棱锥S-ABCD的体积;
(2)求证:面SAB⊥面SBC.
分析:(1)由题意可得SA为四棱锥S-ABCD的高,底面是直角梯形,根据棱锥的体积公式V=
Sh直接求解即可;
(2)先证BC⊥平面SAB,再由面面垂直的判定定理,证明平面SBC⊥平面SAB.
| 1 |
| 3 |
(2)先证BC⊥平面SAB,再由面面垂直的判定定理,证明平面SBC⊥平面SAB.
解答:解:(1)∵SA⊥平面ABCD,∴SA为四棱锥S-ABCD的高,
底面是直角梯形,∠ABC=90°,SA=AB=BC=1,AD=
,
∴棱锥体积:V=
S底•h=
×
(1+
)×1×1=
;
(2)证明:SA⊥底面ABCD,BC?平面ABCD,∴SA⊥BC,
又BC⊥AB,AB∩SA=A,∴BC⊥平面SAB,
∵BC?平面SBC,∴平面SBC⊥平面SAB.
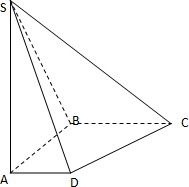
底面是直角梯形,∠ABC=90°,SA=AB=BC=1,AD=
| 1 |
| 2 |
∴棱锥体积:V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
(2)证明:SA⊥底面ABCD,BC?平面ABCD,∴SA⊥BC,
又BC⊥AB,AB∩SA=A,∴BC⊥平面SAB,
∵BC?平面SBC,∴平面SBC⊥平面SAB.

点评:本题考查了面面垂直的判定,考查了棱锥的体积计算,考查考查了学生的空间想象能力,属于基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
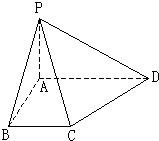 如图,在底面是直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,且
如图,在底面是直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,且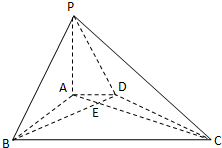 如图,在底面是直角梯形的四棱锥 P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4.AD=2,AB=
如图,在底面是直角梯形的四棱锥 P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4.AD=2,AB= (2012•宿州一模)如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.
(2012•宿州一模)如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.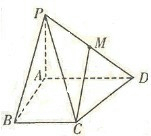 如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面 ABCD,PA=AB=BC=1,AD=2,M为PD中点.
如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面 ABCD,PA=AB=BC=1,AD=2,M为PD中点.