题目内容
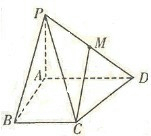 如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面 ABCD,PA=AB=BC=1,AD=2,M为PD中点.
如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面 ABCD,PA=AB=BC=1,AD=2,M为PD中点.( I ) 求证:MC∥平面PAB;
(Ⅱ)在棱PD上找一点Q,使二面角Q-AC-D的正切值为
| ||
| 2 |
分析:(1)欲证MC∥平面PAB,根据线面平行的判定定理可知只需在平面PAB中找一直线与MC平行即可,取PA的中点E,连接BE、EM,根据EM与BC平行且相等,则MC∥BE,又MC?面PAB,BE⊆面PAB,满足定理所需条件;
(2)过Q作QF∥PA交AD于F,作FH⊥AC,H为垂足.连接QH则∠QHF是二面角Q-AC-D的平面角,然后根据二面角Q-AC-D的正切值为
建立等式关系,解之即可求Q在棱PD上的位置.
(2)过Q作QF∥PA交AD于F,作FH⊥AC,H为垂足.连接QH则∠QHF是二面角Q-AC-D的平面角,然后根据二面角Q-AC-D的正切值为
| ||
| 2 |
解答: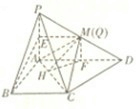 解:(1)取PA的中点E,连接BE、EM,则EM与BC平行且相等,∴四边形BCME是平行四边形.∴MC∥BE,
解:(1)取PA的中点E,连接BE、EM,则EM与BC平行且相等,∴四边形BCME是平行四边形.∴MC∥BE,
又MC?面PAB,BE⊆面PAB,∴MC∥平面PAB…(6分)
(2)如图过Q作QF∥PA交AD于F,
∴QF⊥平面ABCD.作FH⊥AC,H为垂足.连接QH∴∠QHF是二面角Q-AC-D的平面角.
设AF=x,∴AH=FH=
x,FD=2-x.又
=
,∴QF=
,
在Rt△QFH中,tan∠QHF=
=
=
,∴x=1.
当Q为棱PD中点时,二面角Q-AC-D的正切值为
.…(12分)
 解:(1)取PA的中点E,连接BE、EM,则EM与BC平行且相等,∴四边形BCME是平行四边形.∴MC∥BE,
解:(1)取PA的中点E,连接BE、EM,则EM与BC平行且相等,∴四边形BCME是平行四边形.∴MC∥BE,又MC?面PAB,BE⊆面PAB,∴MC∥平面PAB…(6分)
(2)如图过Q作QF∥PA交AD于F,
∴QF⊥平面ABCD.作FH⊥AC,H为垂足.连接QH∴∠QHF是二面角Q-AC-D的平面角.
设AF=x,∴AH=FH=
| ||
| 2 |
| QF |
| PA |
| FD |
| AD |
| 2-x |
| 2 |
在Rt△QFH中,tan∠QHF=
| QF |
| FH |
| ||||
|
| ||
| 2 |
当Q为棱PD中点时,二面角Q-AC-D的正切值为
| ||
| 2 |
点评:本题主要考查了线面平行的判定,以及二面角的度量,同时考查了空间想象能力和论证推理的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
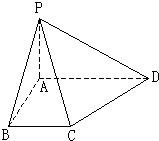 如图,在底面是直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,且
如图,在底面是直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,且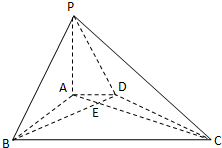 如图,在底面是直角梯形的四棱锥 P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4.AD=2,AB=
如图,在底面是直角梯形的四棱锥 P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4.AD=2,AB= (2012•宿州一模)如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.
(2012•宿州一模)如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.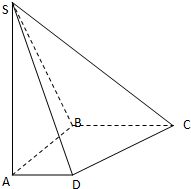 如图,在底面是直角梯形的四棱锥S-ABCD中,
如图,在底面是直角梯形的四棱锥S-ABCD中,