题目内容
 (2012•宿州一模)如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.
(2012•宿州一模)如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.(1)求证:BC⊥平面PAB;
(2)求面PCD与面PAB所成锐二面角的正切值;
(3)在PC上是否存在一点E,使得DE∥平面PAB?若存在,请找出;若不存在,说明理由.
分析:(1)证明BC⊥平面PAB,只需要证明BC垂直于平面PAB内的两条相交直线即可;
(2)延长BA、CD交于Q点,过A作AH⊥PQ,垂足为H,连DH,可证∠AHD是面PCD与面PBA所成的二面角的平面角,求出AH,即可得到面PCD与面PAB所成二面角的正切值;
(3)存在.在BC上取一点F,使BF=1,则DF∥AB,可得DE∥平面PAB.
(2)延长BA、CD交于Q点,过A作AH⊥PQ,垂足为H,连DH,可证∠AHD是面PCD与面PBA所成的二面角的平面角,求出AH,即可得到面PCD与面PAB所成二面角的正切值;
(3)存在.在BC上取一点F,使BF=1,则DF∥AB,可得DE∥平面PAB.
解答: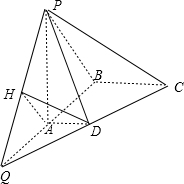 (1)证明:由题意,∵BC∥AD,∠DAB=90°,
(1)证明:由题意,∵BC∥AD,∠DAB=90°,
∴BC⊥AB
∵PA⊥平面ABCD
∴BC⊥PA,又PA∩AB=A
∴BC⊥平面PAB;
(2)解:延长BA、CD交于Q点,过A作AH⊥PQ,垂足为H,连DH
由(1)及AD∥BC知:AD⊥平面PAQ
∴AD⊥PQ且AH⊥PQ
所以PQ⊥平面HAD,即PQ⊥HD.
所以∠AHD是面PCD与面PBA所成的二面角的平面角
∵PA=AB=BC=3,梯形上底AD=1
∴AQ=
,PQ=
,
∴AH=
=
∴tan∠AHD=
=
所以面PCD与面PAB所成二面角的正切值为
(3)解:存在.
在BC上取一点F,使BF=1,则DF∥AB.由条件知,PC=3
,在PC上取点E,使PE=
,则EF∥PB,
所以,平面EFD∥平面PAB,
因为DE?平面EFD,
所以DE∥平面PAB
 (1)证明:由题意,∵BC∥AD,∠DAB=90°,
(1)证明:由题意,∵BC∥AD,∠DAB=90°,∴BC⊥AB
∵PA⊥平面ABCD
∴BC⊥PA,又PA∩AB=A
∴BC⊥平面PAB;
(2)解:延长BA、CD交于Q点,过A作AH⊥PQ,垂足为H,连DH
由(1)及AD∥BC知:AD⊥平面PAQ
∴AD⊥PQ且AH⊥PQ
所以PQ⊥平面HAD,即PQ⊥HD.
所以∠AHD是面PCD与面PBA所成的二面角的平面角
∵PA=AB=BC=3,梯形上底AD=1
∴AQ=
| 3 |
| 2 |
3
| ||
| 2 |
∴AH=
| AQ•PA |
| PQ |
3
| ||
| 5 |
∴tan∠AHD=
| AD |
| AH |
| ||
| 3 |
所以面PCD与面PAB所成二面角的正切值为
| ||
| 3 |
(3)解:存在.
在BC上取一点F,使BF=1,则DF∥AB.由条件知,PC=3
| 3 |
| 3 |
所以,平面EFD∥平面PAB,
因为DE?平面EFD,
所以DE∥平面PAB
点评:本题考查线面垂直,考查面面角,考查存在性问题,解题的关键是掌握线面垂直的判定定理,正确作出面面角.

练习册系列答案
相关题目