题目内容
【题目】若a和b是计算机在区间（0，3）上产生的随机数，那么函数f（x）=lg（ax2+4x+4b） 的值域为R的概率为 ．
【答案】
【解析】解：由已知，a和b是计算机在区间（0，3）上产生的随机数，对应区域的面积为4， 因为函数f（x）=lg（ax2+4x+4b）的值域为R（实数集），所以（ax2+4x+4b）能取得所有的正数，
所以 
，解得ab≤1且a＞0，
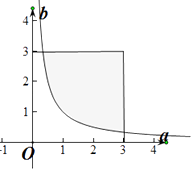
对应的区域面积为
9﹣ 
（3﹣ 
）da=9﹣（3a﹣lna）| 
=1+2ln3；
由几何概型的公式得：
所以答案是： 
【考点精析】关于本题考查的几何概型，需要了解几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等才能得出正确答案．
练习册系列答案
相关题目
