题目内容
已知定义域为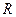 的函数
的函数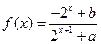 是奇函数。
是奇函数。
(Ⅰ)求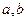 的值;
的值;
(Ⅱ)若对任意的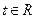 ,不等式
,不等式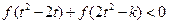 恒成立,求
恒成立,求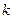 的取值范围;
的取值范围;
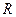 的函数
的函数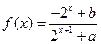 是奇函数。
是奇函数。(Ⅰ)求
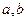 的值;
的值;(Ⅱ)若对任意的
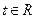 ,不等式
,不等式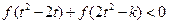 恒成立,求
恒成立,求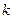 的取值范围;
的取值范围;⑴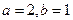 ⑵
⑵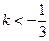
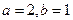 ⑵
⑵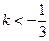
(Ⅰ)因为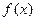 是奇函数,所以
是奇函数,所以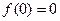 ,即
,即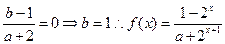
又由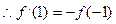 知
知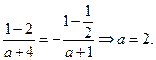
(Ⅱ)[解法一]由(Ⅰ)知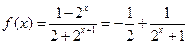 ,易知
,易知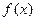 在
在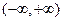 上
上
为减函数。又因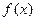 是奇函数,从而不等式:
是奇函数,从而不等式: 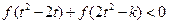
等价于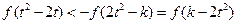 ,因
,因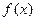 为减函数,由上式推得:
为减函数,由上式推得:
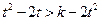 .即对一切
.即对一切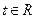 有:
有: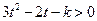 ,
,
从而判别式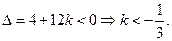
[解法二]由(Ⅰ)知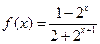 .又由题设条件得:
.又由题设条件得:
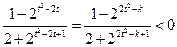 ,
,
即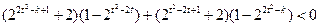 ,
,
整理得
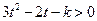
上式对一切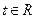 均成立,从而判别式
均成立,从而判别式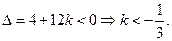
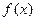 是奇函数,所以
是奇函数,所以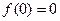 ,即
,即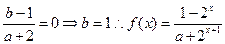
又由
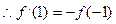 知
知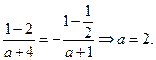
(Ⅱ)[解法一]由(Ⅰ)知
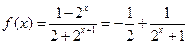 ,易知
,易知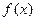 在
在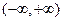 上
上为减函数。又因
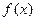 是奇函数,从而不等式:
是奇函数,从而不等式: 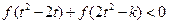
等价于
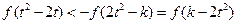 ,因
,因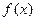 为减函数,由上式推得:
为减函数,由上式推得: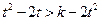 .即对一切
.即对一切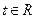 有:
有: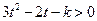 ,
,从而判别式
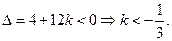
[解法二]由(Ⅰ)知
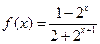 .又由题设条件得:
.又由题设条件得: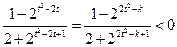 ,
,即
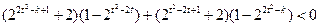 ,
,整理得

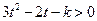
上式对一切
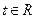 均成立,从而判别式
均成立,从而判别式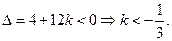

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
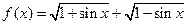 ,
,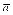 是函数的一个周期。
是函数的一个周期。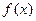

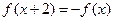
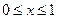 时,
时,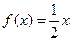 ,求使
,求使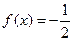 在
在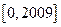 上的
上的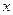 的个数
的个数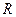 上的函数
上的函数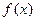 不是常数函数,且满足对任意的
不是常数函数,且满足对任意的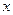 ,
,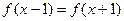 ,
,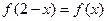 ,现得出下列5个结论:①
,现得出下列5个结论:①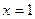 对称,③
对称,③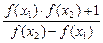 ;
; 求证:
求证: 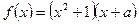 为奇函数,则
为奇函数,则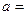 ___________。
___________。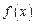 是
是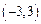 上的奇函数,当
上的奇函数,当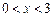 时,
时,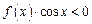 的解集是( )
的解集是( )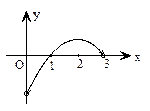
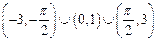
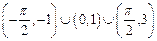
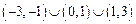
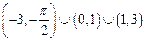
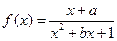 在
在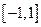 上是奇函数,则
上是奇函数,则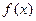 的解析式为________.
的解析式为________.