题目内容
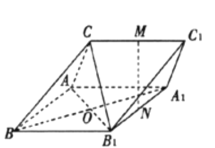
【题目】设直线![]() 与直线
与直线![]() 分别与椭圆
分别与椭圆![]()
![]() 交于点
交于点![]() ,且四边形
,且四边形![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,是否存在经过原点,且以
两点,是否存在经过原点,且以![]() 为直径的圆?若有,请求出圆的方程,若没有,请说明理由.
为直径的圆?若有,请求出圆的方程,若没有,请说明理由.
【答案】(1)![]() ;(2)存在,圆的方程为
;(2)存在,圆的方程为 .
.
【解析】
(1)根据两条直线解析式特征可知直线![]() 与直线
与直线![]() 关于坐标轴对称,则
关于坐标轴对称,则![]() 为矩形,将
为矩形,将![]() 与椭圆方程联立,表示出交点的横纵坐标,即可由四边形
与椭圆方程联立,表示出交点的横纵坐标,即可由四边形![]() 的面积确定参数,求得椭圆
的面积确定参数,求得椭圆![]() 的方程;
的方程;
(2)设直线![]() 的方程
的方程![]() ,两个交点坐标
,两个交点坐标![]() .联立椭圆方程后化简,用韦达定理表示出
.联立椭圆方程后化简,用韦达定理表示出![]() ,经过原点,且以
,经过原点,且以![]() 为直径的圆满足
为直径的圆满足![]() ,即
,即![]() ,由平面向量数量积的坐标运算代入即可求得斜率
,由平面向量数量积的坐标运算代入即可求得斜率![]() .由中点坐标公式即可求得线段
.由中点坐标公式即可求得线段![]() 中点
中点![]() 的坐标,进而求得
的坐标,进而求得![]() 的值,即可得圆的标准方程.
的值,即可得圆的标准方程.
(1)由题意可知直线![]() 与直线
与直线![]() 关于坐标轴对称,所以四边形
关于坐标轴对称,所以四边形![]() 为矩形,
为矩形,
则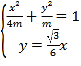 ,解得
,解得![]()
所以![]() ,
,
解得![]() ,
,
代入椭圆方程可得![]() .
.
(2)存在.
设![]() ,由题意可知直线
,由题意可知直线![]() 的斜率必然存在.
的斜率必然存在.
直线![]() 过点
过点![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,
,
则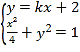 ,化简可得
,化简可得![]() ,
,
所以![]() ,
,
经过原点,且以![]() 为直径的圆满足
为直径的圆满足![]() ,即
,即![]() ,
,
则![]()
![]()
![]()
![]()
![]() ,
,
解方程可得![]() ,经检验可知都满足
,经检验可知都满足![]() .
.
设线段![]() 的中点为
的中点为![]() .
.
则![]()
![]()
所以![]() ,
,
所以存在满足条件的圆,圆的方程为 .
.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如表:
质量指标值m | 25≤m<35 | 15≤m<25或35≤m<45 | 0<m<15或45≤m<65 |
等级 | 一等品 | 二等品 | 三等品 |
某企业从生产的这种产品中抽取100件产品作为样本,检测其质量指标值,得到下图的率分布直方图.(同一组数据用该区间的中点值作代表)
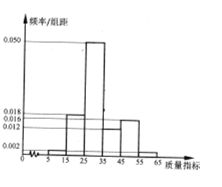
(1)该企业为提高产品质量,开展了质量提升月”活动,活动后再抽样检测,产品三等品数Y近似满足Y~H(10,15,100),请测算“质量提升月”活动后这种产品的“二等品率“(一、二等品其占全部产品百分比)较活动前提高多少个百分点?
(2)若企业每件一等品售价180元,每件二等品售价150元,每件三等品售价120元,以样本中的频率代替相应概率,现有一名联客随机购买两件产品,设其支付的费用为X(单位:元),求X的分布列及数学期望.
【题目】在某区“创文明城区”(简称“创城”)活动中,教委对本区![]() 四所高中学校按各校人数分层抽样,随机抽查了100人,将调查情况进行整理后制成下表:
四所高中学校按各校人数分层抽样,随机抽查了100人,将调查情况进行整理后制成下表:
学校 |
|
|
|
|
抽查人数 | 50 | 15 | 10 | 25 |
“创城”活动中参与的人数 | 40 | 10 | 9 | 15 |
(注:参与率是指:一所学校“创城”活动中参与的人数与被抽查人数的比值)假设每名高中学生是否参与”创城”活动是相互独立的.
(1)若该区共2000名高中学生,估计![]() 学校参与“创城”活动的人数;
学校参与“创城”活动的人数;
(2)在随机抽查的100名高中学生中,随机抽取1名学生,求恰好该生没有参与“创城”活动的概率;
(3)在上表中从![]() 两校没有参与“创城”活动的同学中随机抽取2人,求恰好
两校没有参与“创城”活动的同学中随机抽取2人,求恰好![]() 两校各有1人没有参与“创城”活动的概率是多少?
两校各有1人没有参与“创城”活动的概率是多少?