题目内容
【题目】选修4-4：坐标系与参数方程
在平面直角坐标系中，以坐标原点为极点，以
轴正半轴为极轴，建立极坐标系，点
的极坐标为
，直线
的极坐标方程为
，且
过点
，曲线
的参数方程为
(
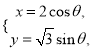为参数).
(Ⅰ)求曲线
上的点到直线
的距离的最大值；
(Ⅱ)过点
与直线
平行的直线
与曲线 
交于
两点，求
的值.
【答案】（Ⅰ）
；(Ⅱ) 
.
【解析】试题分析：（1）由直角坐标与极坐标互换公式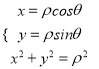
，可得直线
的直角坐标方程为
，再由点到直线的距离公式及辅助角公式可求得最值。（2）直线
的参数方程为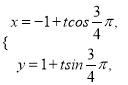
（
为参数），代入曲线
的普通方程为
.由参数t的几何意义可得
。
试题解析：(Ⅰ)由直线
过点
可得
，故
，
则易得直线
的直角坐标方程为
根据点到直线的距离方程可得曲线
上的点到直线
的距离
，
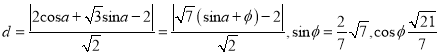(Ⅱ)由（1）知直线
的倾斜角为
，
则直线
的参数方程为
（
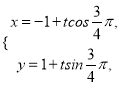为参数）.
又易知曲线
的普通方程为
.
把直线
的参数方程代入曲线
的普通方程可得
，
，依据参数
的几何意义可知
.
【题目】某种产品的质量以其质量指标值衡量，并依据质量指标值划分等级如表：
质量指标值m | 25≤m＜35 | 15≤m＜25或35≤m＜45 | 0＜m＜15或45≤m＜65 |
等级 | 一等品 | 二等品 | 三等品 |
某企业从生产的这种产品中抽取100件产品作为样本，检测其质量指标值，得到下图的率分布直方图．（同一组数据用该区间的中点值作代表）
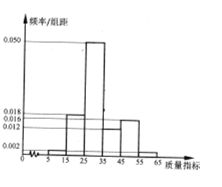
（1）该企业为提高产品质量，开展了质量提升月”活动，活动后再抽样检测，产品三等品数Y近似满足Y～H（10，15，100），请测算“质量提升月”活动后这种产品的“二等品率“（一、二等品其占全部产品百分比）较活动前提高多少个百分点？
（2）若企业每件一等品售价180元，每件二等品售价150元，每件三等品售价120元，以样本中的频率代替相应概率，现有一名联客随机购买两件产品，设其支付的费用为X（单位：元），求X的分布列及数学期望．
