题目内容
【题目】对于集合![]() ,
,![]() ,
,![]() ,
,![]() ,定义
,定义![]() .
.
集合![]() 中的元素个数记为
中的元素个数记为![]() ,当
,当![]() ,称集合
,称集合![]() 具有性质
具有性质![]() .
.
(1)已知集合![]() ,
,![]() ,写出
,写出![]() ,
,![]() 的值,并判断集合
的值,并判断集合![]() 是否具有性质
是否具有性质![]() ;
;
(2)设集合![]() 具有性质
具有性质![]() ,判断集合
,判断集合![]() 中的三个元素是否能组成等差数列,请说明理由;
中的三个元素是否能组成等差数列,请说明理由;
(3)若数列![]() 是以
是以![]() 为首项,2为公比的等比数列. 数列
为首项,2为公比的等比数列. 数列![]() 中的前100项:
中的前100项:![]() 组成的集合
组成的集合![]() 记作
记作![]() ,将集合
,将集合![]() 中的所有元素
中的所有元素![]() 从小到大排序,即
从小到大排序,即![]() 满足
满足![]() ,求
,求![]() .
.
【答案】(1)集合![]() 不具有性质
不具有性质![]() ;(2)
;(2)![]() 中的三个元素不能构成等差数列,见解析;(3)2816
中的三个元素不能构成等差数列,见解析;(3)2816
【解析】
(1)根据定义分别计算![]() 和
和![]() ,再判断集合
,再判断集合![]() 是否具有性质
是否具有性质![]() 即可.
即可.
(2)根据集合![]() 具有性质
具有性质![]() 可知
可知![]() 中的元素应是:
中的元素应是:![]() 这6个元素应该互不相等. 再根据等差数列的性质判定矛盾即可.
这6个元素应该互不相等. 再根据等差数列的性质判定矛盾即可.
(3)易得![]() ,进而可得
,进而可得![]() ,再根据指数的运算可推导出当
,再根据指数的运算可推导出当![]() 时,
时,![]() ,且
,且![]() ,进而将集合
,进而将集合![]() 中的所有元素进行排序,再求
中的所有元素进行排序,再求![]() 即可.
即可.
(1)因为![]() ,
,![]() ,所以根据题目中的定义可知
,所以根据题目中的定义可知![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
又![]() ,而
,而![]() ,所以集合
,所以集合![]() 不具有性质
不具有性质![]() .
.
(2)集合![]() 中的三个元素不能组成等差数列,理由如下:因为集合
中的三个元素不能组成等差数列,理由如下:因为集合![]() 具有性质
具有性质![]() ,所以
,所以![]() ,
,
由题中所给的定义可知:![]() 中的元素应是:
中的元素应是:![]() 这6个元素应该互不相等.
这6个元素应该互不相等.
假设![]() 中的三个元素能构成等差数列,
中的三个元素能构成等差数列,
若![]() 为等差中项,则
为等差中项,则![]() ,而
,而![]() 均为其中的元素,这与集合中的6个元素互不相等矛盾;
均为其中的元素,这与集合中的6个元素互不相等矛盾;
若![]() 或
或![]() 为等差中项,同理,矛盾.
为等差中项,同理,矛盾.
故![]() 中的三个元素不能构成等差数列.
中的三个元素不能构成等差数列.
(3)因为数列![]() 是以
是以![]() 为首项,2为公比的等比数列,所以
为首项,2为公比的等比数列,所以![]() .
.
则![]() ,因为
,因为![]() 是单调递增数列,
是单调递增数列,
若![]() ,即
,即![]() ,即
,即![]() ,则
,则![]() ,
,
又![]() ,所当
,所当![]() 时,
时,![]() ,且
,且![]() .
.
故根据定义将集合![]() 中的所有元素从小到大排序为:
中的所有元素从小到大排序为:
![]()
所以小于等于![]() 的元素个数为:
的元素个数为:![]() ,
,
当![]() 时,即小于等于
时,即小于等于![]() 的数共有91个数,显然不到100个数,所以第100个数为
的数共有91个数,显然不到100个数,所以第100个数为![]() .
.
因此![]() .
.

【题目】近年来,随着国家综合国力的提升和科技的进步,截至2018年底,中国铁路运营里程达13,2万千米,这个数字比1949年增长了5倍;高铁运营里程突破2.9万千米,占世界高铁运营里程的60%以上,居世界第一位下表截取了2012--2016年中国高铁密度的发展情况(单位:千米/万平方千米).
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
高铁密度 | 9.75 | 11.49 | 17.14 | 20.66 | 22.92 |
已知高铁密度y与年份代码x之间满足关系式![]() (
(![]() 为大于0的常数)若对
为大于0的常数)若对![]() 两边取自然对数,得到
两边取自然对数,得到![]() ,可以发现
,可以发现![]() 与
与![]() 线性相关.
线性相关.
(1)根据所给数据,求y关于x的回归方程(![]() 保留到小数点后一位);
保留到小数点后一位);
(2)利用(1)的结论,预测到哪一年高铁密度会超过30千米/平方千米.
参考公式设具有线性相关系的两个变量![]() 的一组数据为
的一组数据为![]() ,
,
则回归方程![]() 的系数:
的系数: ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如表:
质量指标值m | 25≤m<35 | 15≤m<25或35≤m<45 | 0<m<15或45≤m<65 |
等级 | 一等品 | 二等品 | 三等品 |
某企业从生产的这种产品中抽取100件产品作为样本,检测其质量指标值,得到下图的率分布直方图.(同一组数据用该区间的中点值作代表)
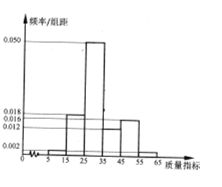
(1)该企业为提高产品质量,开展了质量提升月”活动,活动后再抽样检测,产品三等品数Y近似满足Y~H(10,15,100),请测算“质量提升月”活动后这种产品的“二等品率“(一、二等品其占全部产品百分比)较活动前提高多少个百分点?
(2)若企业每件一等品售价180元,每件二等品售价150元,每件三等品售价120元,以样本中的频率代替相应概率,现有一名联客随机购买两件产品,设其支付的费用为X(单位:元),求X的分布列及数学期望.