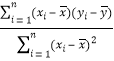题目内容
【题目】用“五点法”画出下列函数的图像,并指出该函数图像怎样由函数![]() 的图像变换得到.
的图像变换得到.
(1)![]() ;
;
(2)![]() .
.
【答案】(1)见解析(2)见解析
【解析】
(1)化简![]() ,列出表格,画出图像,再根据三角函数平移法则得到答案.
,列出表格,画出图像,再根据三角函数平移法则得到答案.
(2)列出表格,画出图像,变换![]() ,再根据三角函数平移法则得到答案.
,再根据三角函数平移法则得到答案.
(1)![]() ,如表所示:
,如表所示:
| 0 |
|
|
|
|
|
|
|
|
|
|
| 0 | 2 | 0 |
| 0 |
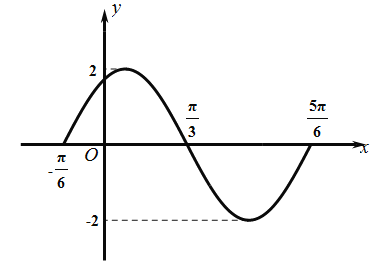
在平面直角坐标系中,作出函数![]() 的图像(如图).
的图像(如图).
从图像变换看,可由![]() 图像上所有点先向左平移
图像上所有点先向左平移![]() 个单位,得到
个单位,得到![]() 的图像;然后把图像上点的横坐标缩短为原来的
的图像;然后把图像上点的横坐标缩短为原来的![]() ,纵坐标不变,得到函数
,纵坐标不变,得到函数![]() 的图像;再把所得图像上点的纵坐标伸长为原来的2倍,横坐标不变,即得到
的图像;再把所得图像上点的纵坐标伸长为原来的2倍,横坐标不变,即得到![]() 的图像.
的图像.
(2)如表所示:
| 0 |
|
|
|
|
|
|
|
|
|
|
| 2 | 0 |
| 0 | 2 |
要由![]() 的图像变换得到
的图像变换得到![]() 的图像,则首先要对目标函数进行转化,即
的图像,则首先要对目标函数进行转化,即![]() .
.
先将![]() 图像上所有点向左平移
图像上所有点向左平移![]() 个单位,得到
个单位,得到![]() 的图像;然后把图像上点的横坐标伸长为原来的2倍,纵坐标不变,得到函数
的图像;然后把图像上点的横坐标伸长为原来的2倍,纵坐标不变,得到函数![]() 的图像;再把所得图像上点的纵坐标伸长为原来的2倍,横坐标不变,即得到
的图像;再把所得图像上点的纵坐标伸长为原来的2倍,横坐标不变,即得到![]() 的图像,如图所示.
的图像,如图所示.
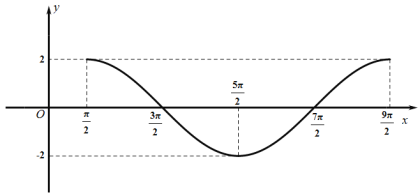

 高中必刷题系列答案
高中必刷题系列答案【题目】某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
空气质量指数 |
|
|
|
|
|
|
空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
该社团将该校区在2018年11月中10天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.

(Ⅰ)以这10天的空气质量指数监测数据作为估计2018年11月的空气质量情况,则2018年11月中有多少天的空气质量达到优良?
(Ⅱ)已知空气质量等级为1级时不需要净化空气,空气质量等级为2级时每天需净化空气的费用为1000元,空气质量等量等级为3级时每天需净化空气的费用为2000元.若从这10天样本中空气质量为1级、2级、3级的天数中任意抽取两天,求这两天的净化空气总费用为3000元的概率.