题目内容
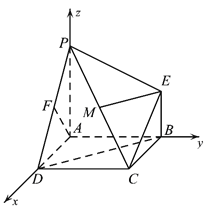
【题目】如图,四边形![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() //
// ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.

(1)求证: ![]() ;
;
(2)求证: ![]() //平面
//平面![]() ;
;
(3)求二面角![]() 的大小.
的大小.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】试题分析:(1)以![]() 为原点,分别以
为原点,分别以![]() 、
、![]() 、
、![]() 的方向为
的方向为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正方向建立空间直角坐标系.求出相关点的坐标,通过计算
轴的正方向建立空间直角坐标系.求出相关点的坐标,通过计算![]() ,证明
,证明![]() ;(2)取
;(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,证明
,证明![]() ,然后证明
,然后证明![]() 平面
平面![]() ;(3)求出平面
;(3)求出平面![]() 的一个法向量,平面
的一个法向量,平面![]() 的法向量,利用空间向量的数量积求解二面角
的法向量,利用空间向量的数量积求解二面角![]() 的余弦值.
的余弦值.
试题解析:(1)证明:依题意, ![]() 平面
平面![]() ,如图,以
,如图,以![]() 为原点,分别以
为原点,分别以![]() 、
、![]() 、
、![]() 的方向为
的方向为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正方向建立空间直角坐标系.
轴的正方向建立空间直角坐标系.
依题意,可得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,因为
,因为![]() ,
, ![]() ,所以
,所以![]() .
.
所以![]() .
.
(2)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
因为![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,所以
,所以![]() .
.
又因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(3)解:因为![]() ,
, ![]() ,
,
![]() ,
,
所以![]() 平面
平面![]() ,故
,故![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
设平面![]() 的法向量为
的法向量为![]() ,
,
因为![]() ,
, ![]() ,
,
所以![]() 即
即![]()
令![]() ,得
,得![]() ,
, ![]() ,故
,故![]() .
.
所以![]() ,所以二面角
,所以二面角![]() 的大小为
的大小为![]() .
.

练习册系列答案
相关题目
【题目】某市A,B,C,D四所中学报名参加某高校2015年自主招生考试的学生人数如下表所示:
中学 | A | B | C | D |
人数 | 40 | 30 | 10 | 20 |
该市教委为了解参加考试的学生的学习状况,采用分层抽样的方法从四所中学报名参加考试的学生中随机抽取50名参加问卷调查.则A,B,C,D四所中学抽取的学生人数分别为( )
A.15,20,10,5B.15,20,5,10
C.20,15,10,5D.20,15,5,10


