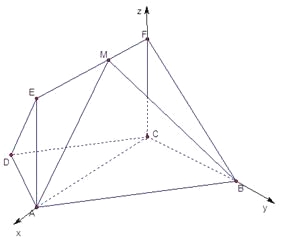
题目内容
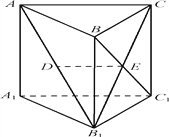
【题目】如图,在梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
, ![]() .
.
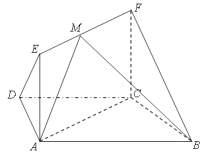
(1)求证: ![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动,设平面
上运动,设平面![]() 与平面
与平面![]() 所成二面角的平面角为
所成二面角的平面角为![]() ,试求
,试求![]() 的取值范围.
的取值范围.
【答案】(1)详见解析;(2)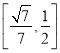 .
.
【解析】试题分析:(1)根据条件证明![]() ,再由面面垂直的判定即可求解;(2)建立空间直角坐标系,求得两个平面的法向量后即可建立二面角余弦值的函数关系式,求得函数的值域即可求解.
,再由面面垂直的判定即可求解;(2)建立空间直角坐标系,求得两个平面的法向量后即可建立二面角余弦值的函数关系式,求得函数的值域即可求解.
试题解析:(1)在梯形![]() 中, ∵
中, ∵![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ;(2)由(1)可建立分别以直线
;(2)由(1)可建立分别以直线![]() ,
, ![]() ,
, ![]() 为
为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴,如图所示空间直角坐标系,令
轴,如图所示空间直角坐标系,令![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,设
,设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
由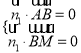 得
得 ,取
,取![]() ,则
,则![]() ,
,
∵![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
∴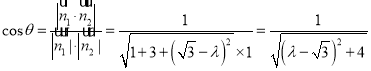 ,
,
∵![]() ,∴当
,∴当![]() 时,
时,![]() 有最小值
有最小值![]() ,
,
当![]() 时,
时,![]() 有最大值
有最大值![]() ,∴
,∴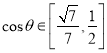 .
.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
【题目】为了普及法律知识,达到“法在心中”的目的,某市法制办组织了普法知识竞赛.统计局调查队随机抽取了甲、乙两单位中各5名职工的成绩,成绩如下表:
甲单位 | 87 | 88 | 91 | 91 | 93 |
乙单位 | 85 | 89 | 91 | 92 | 93 |
(1)根据表中的数据,分别求出甲、乙两单位职工成绩的平均数和方差,并判断哪个单位对法律知识的掌握更稳定;
(2)用简单随机抽样法从乙单位5名职工中抽取2名,他们的成绩组成一个样本,求抽取的2名职工的分数差至少是4的概率.