题目内容
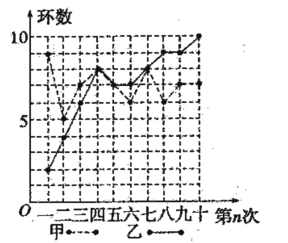
【题目】甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
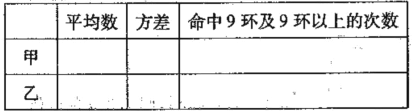
(Ⅰ)请填写下表(写出计算过程):
(Ⅱ)从下列三个不同的角度对这次测试结果进行分析;
①从平均数和方差相结合看(分析谁的成绩更稳定);
②从平均数和命中9环及9环以上的次数相结合看(分析谁的成绩好些);
③从折线图上两人射击命中环数的走势看(分析谁更有潜力)
【答案】(Ⅰ)见解析;(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)由折线图,求出甲设计![]() 次中靶环数和乙射击
次中靶环数和乙射击![]() 次中靶环数,由此能求出结果;(Ⅱ)①由平均数相同,
次中靶环数,由此能求出结果;(Ⅱ)①由平均数相同,![]() ,知甲成绩比乙稳定;②由平均数相同,命中9环及9环以上的次数甲比乙少,知乙成绩比甲好些;③乙处于上升势头,从第四次以后就没有比甲少的情况发生,乙较有潜力.
,知甲成绩比乙稳定;②由平均数相同,命中9环及9环以上的次数甲比乙少,知乙成绩比甲好些;③乙处于上升势头,从第四次以后就没有比甲少的情况发生,乙较有潜力.
试题解析:由折线图,知
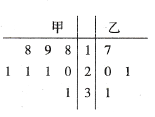
甲射击10次中靶环数分别为:9,5,7,8,7,6,8,6,7,7.
将它们由小到大重排为:5,6,6,7,7,7,7,8,8,9.
乙射击10次中靶环数分别为:2,4,6,8,7,7,8,9,9,10.也将它们由小到大重排为:2,4,6,7,7,8,8,9,9,10.
(Ⅰ)![]() (环),
(环),
![]() (环)
(环)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
根据以上的分析与计算填表如下:
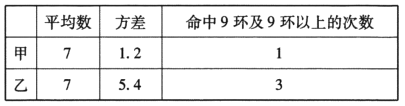
(Ⅱ)①∵平均数相同,![]() ,
,
∴甲成绩比乙稳定.
②∵平均数相同,命中9环及9环以上的次数甲比乙少,
∴乙成绩比甲好些.
③甲成绩在平均数上下波动;而乙处于上升势头,从第四次以后就没有比甲少的情况发生,乙较有潜力.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】探究函数![]() ,
,![]() 上的最小值,并确定取得最小值时
上的最小值,并确定取得最小值时![]() 的值,列表如下:
的值,列表如下:
| … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| … | 14 | 7 | 5.34 | 5.11 | 5.01 | 5 | 5.01 | 5.04 | 5.08 | 5.67 | 7 | 8.6 | 12.14 | … |
(1)观察表中![]() 值随
值随![]() 值变化趋势特点,请你直接写出函数
值变化趋势特点,请你直接写出函数![]() ,
,![]() 的单调区间,并指出当
的单调区间,并指出当![]() 取何值时函数的最小值为多少;
取何值时函数的最小值为多少;
(2)用单调性定义证明函数![]() 在
在![]() 上的单调性.
上的单调性.
【题目】已知椭圆![]() ,抛物线
,抛物线![]() 的焦点均在
的焦点均在![]() 轴上,
轴上, ![]() 的中心和
的中心和![]() 的顶点均为原点
的顶点均为原点![]() ,从
,从![]() ,
, ![]() 上分别取两个点,将其坐标记录于下表中:
上分别取两个点,将其坐标记录于下表中:
| 3 | -2 | 4 |
|
|
| 0 | -4 |
|
(1)求![]() 的标准方程;
的标准方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,且线段
,且线段![]() 的垂直平分线过定点
的垂直平分线过定点![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.