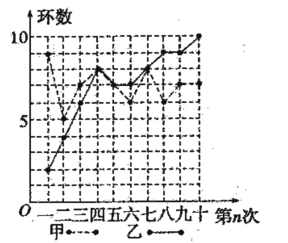
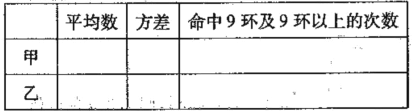
题目内容
【题目】已知椭圆![]() ,抛物线
,抛物线![]() 的焦点均在
的焦点均在![]() 轴上,
轴上, ![]() 的中心和
的中心和![]() 的顶点均为原点
的顶点均为原点![]() ,从
,从![]() ,
, ![]() 上分别取两个点,将其坐标记录于下表中:
上分别取两个点,将其坐标记录于下表中:
| 3 | -2 | 4 |
|
|
| 0 | -4 |
|
(1)求![]() 的标准方程;
的标准方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,且线段
,且线段![]() 的垂直平分线过定点
的垂直平分线过定点![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() :
: ![]() .
.![]() ;(2)
;(2) 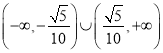 .
.
【解析】试题分析:(1)先分析出点![]() ,
, ![]() 在抛物线上,点
在抛物线上,点![]() ,
, ![]() 在椭圆上,利用待定系数法可得到
在椭圆上,利用待定系数法可得到![]() 的标准方程;(2)设
的标准方程;(2)设![]() ,
, ![]() ,将
,将![]() 代入椭圆方程,消去
代入椭圆方程,消去![]() 得
得![]() ,利用韦达定理以及中点坐标公式可得线段
,利用韦达定理以及中点坐标公式可得线段![]() 的垂直平分线
的垂直平分线![]() 的方程为
的方程为![]() ,由点
,由点![]() 在直线
在直线![]() 上,得
上,得![]() ,结合判别式大于零可得实数
,结合判别式大于零可得实数![]() 的取值范围.
的取值范围.
试题解析::(1)设抛物线![]() ,则有
,则有![]() ,据此验证4个点知
,据此验证4个点知![]() ,
, ![]() 在抛物线上,易求
在抛物线上,易求![]() .
.
设![]() ,把点
,把点![]() ,
, 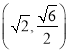 代入得:
代入得:
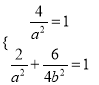 ,解得
,解得![]() ,所以
,所以![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
, ![]() ,将
,将![]() 代入椭圆方程,消去
代入椭圆方程,消去![]() 得
得![]() ,
,
所以![]() ,即
,即![]() .①
.①
由根与系数关系得![]() ,则
,则![]() ,
,
所以线段![]() 的中点
的中点![]() 的坐标为
的坐标为![]() .
.
又线段![]() 的垂直平分线
的垂直平分线![]() 的方程为
的方程为![]() ,
,
由点![]() 在直线
在直线![]() 上,得
上,得![]() ,
,
即![]() ,所以
,所以![]() ,
,
由①得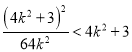 ,所以
,所以![]() ,即
,即![]() 或
或![]() ,
,
所以实数![]() 的取值范围是
的取值范围是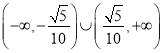 .
.

练习册系列答案
相关题目