题目内容
设二次函数f(x)=x2+bx+c(b,c∈R),已知α,β不论为何实数恒有f(sinα)≥0,f(2+cosβ)≤0,
(1)求证:b+c+1=0;
(2)求证c≥3;
(3)若函数f(sinα)的最大值为8,求b,c值。
(1)求证:b+c+1=0;
(2)求证c≥3;
(3)若函数f(sinα)的最大值为8,求b,c值。
解:(1)∵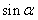 ∈[-1,1],2+
∈[-1,1],2+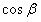 ∈[1,3],
∈[1,3],
又∵f( )≥0,f(2+
)≥0,f(2+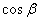 )≤0恒成立,
)≤0恒成立,
∴f(1)≥0,f(1)≤0,
即f(1)=0,
∴1+b+c=0。
(2)∵f(3)≤0,
∴9+3b+c≤0,
∴9+3(-1-c)+c≤0,
∴c≥3。
(3)由题意可知:f(x)在[-1,1]上为减函数,
∴8=f(-1)=1-b+c, ①
又b+c=-1, ②
联立①②,得b=-4,c=3。
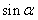 ∈[-1,1],2+
∈[-1,1],2+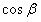 ∈[1,3],
∈[1,3],又∵f(
 )≥0,f(2+
)≥0,f(2+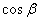 )≤0恒成立,
)≤0恒成立,∴f(1)≥0,f(1)≤0,
即f(1)=0,
∴1+b+c=0。
(2)∵f(3)≤0,
∴9+3b+c≤0,
∴9+3(-1-c)+c≤0,
∴c≥3。
(3)由题意可知:f(x)在[-1,1]上为减函数,
∴8=f(-1)=1-b+c, ①
又b+c=-1, ②
联立①②,得b=-4,c=3。

练习册系列答案
相关题目
设二次函数f(x)=ax2+bx+c(a>0),方程f(x)-x=0的两个根x1、x2满足0<x1<x2<
,且函数f(x)的图象关于直线x=x0对称,则有( )
| 1 |
| a |
A、x0≤
| ||
B、x0>
| ||
C、x0<
| ||
D、x0≥
|