题目内容
15.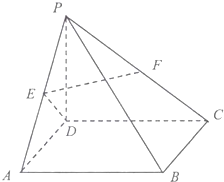 如图,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PD⊥底面ABCD,PD=DA,E、F分别为PA、PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PD⊥底面ABCD,PD=DA,E、F分别为PA、PC的中点.(1)求证:EF∥平面ABCD;
(2)求证:DE⊥平面PAB.
分析 (1)连接AC,根据中位线定理可得EF∥AC,结合线面平行的判定定理,可得EF∥平面ABCD;
(2)先结合已知证明平面PAD⊥平面PAB,再由面面垂直的性质定理可得DE⊥平面PAB.
解答 证明:(1)连接AC,如图所示: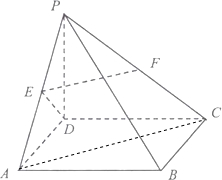
∵E、F分别为PA、PC的中点.
∴EF∥AC,
又∵EF?平面ABCD,AC?平面ABCD,
∴EF∥平面ABCD;
(2)∵底面ABCD为正方形,侧棱PD⊥底面ABCD,
∴PD⊥AB,AD⊥AB,
又∵PD∩AD=D,PD,AD?平面PAD,
∴AB⊥平面PAD,
又∵AB?平面PAB,
∴平面PAD⊥平面PAB,
∵PD=DA,E为PA的中点.
∴DE⊥PA,
∵平面PAD∩平面PAB=PA,
∴DE⊥平面PAB.
点评 本题考查的知识点是线面平行的判定,线面垂直,面面垂直与线线垂直的相互转化,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.m,n,l是直线,α,β是两个不同的平面,下面说法正确的是( )
| A. | 若m∥α,m∥β,则α∥β | |
| B. | 若m⊥α,m?β,则α⊥β | |
| C. | 若m?α,n?α,m,n是异面直线,则n与α相交 | |
| D. | 若m?α,n?α,l⊥m,l⊥n,则l⊥α |
10.下列图象表示的函数中,不能用二分法求零点的是( )
| A. |  | B. | 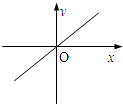 | C. |  | D. | 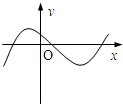 |
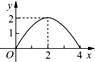
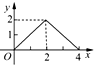
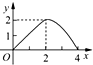
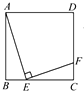 如图,已知正方形ABCD的边长为4,E是BC边上的一个动点,AE⊥EF,EF交DC于F,设BE=x,FC=y,则当点E从点B运动到点C时,y关于x的函数图象是( )
如图,已知正方形ABCD的边长为4,E是BC边上的一个动点,AE⊥EF,EF交DC于F,设BE=x,FC=y,则当点E从点B运动到点C时,y关于x的函数图象是( )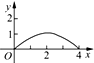
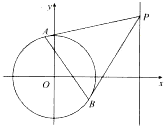 已知圆C的圆心为原点O,且与直线$x+y+4\sqrt{3}=0$相切.
已知圆C的圆心为原点O,且与直线$x+y+4\sqrt{3}=0$相切.