题目内容
6.sinx+$\sqrt{3}$cosx=a在区间(0,2π)内的个相异的实数根x1,x2.(1)求a的取值范围;
(2)求x1+x2的值.
分析 (1)令f(x)=sinx+$\sqrt{3}$cosx=2sin(x+$\frac{π}{3}$),x∈(0,2π),画出函数的图象,可得满足条件的a的取值范围;
(2)结合(1)中函数的对称性,可得x1+x2的值.
解答 解:(1)令f(x)=sinx+$\sqrt{3}$cosx=2sin(x+$\frac{π}{3}$),x∈(0,2π),
则函数f(x)的图象如下图所示: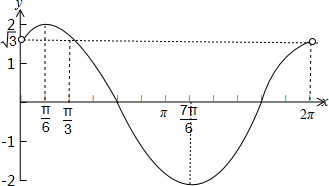
由图可得:若sinx+$\sqrt{3}$cosx=a在区间(0,2π)内的个相异的实数根x1,x2.
则a∈(-2,$\sqrt{3}$)∪($\sqrt{3}$,2);
(2)当a∈(-2,$\sqrt{3}$)时,x1,x2关于x=$\frac{7π}{6}$对称,x1+x2=$\frac{7π}{3}$;
当a∈($\sqrt{3}$,2)时,x1,x2关于x=$\frac{π}{6}$对称,x1+x2=$\frac{π}{3}$;
点评 本题考查的知识点是三角函数的图象和性质,和差角(辅助角)公式,其中利用和差角(辅助角)公式将函数解析式化简,是解答的关键.

练习册系列答案
相关题目
14.计算:4lg2+3lg5-lg$\frac{1}{5}$的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8.已知0<α<$\frac{π}{2}$,则sinα,α,tanα的大小关系为( )
| A. | tanα>sinα>α | B. | α>tanα>sinα | C. | sinα>α>tanα | D. | tanα>α>sinα |
6.m,n,l是直线,α,β是两个不同的平面,下面说法正确的是( )
| A. | 若m∥α,m∥β,则α∥β | |
| B. | 若m⊥α,m?β,则α⊥β | |
| C. | 若m?α,n?α,m,n是异面直线,则n与α相交 | |
| D. | 若m?α,n?α,l⊥m,l⊥n,则l⊥α |