题目内容
(本小题满分14分)
如图,直线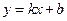 与椭圆
与椭圆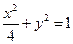 交于
交于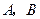 两点,记
两点,记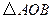 的面积为
的面积为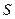 .
.
(I)求在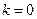 ,
,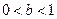 的条件下,
的条件下,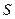 的最大值;
的最大值;
(II)当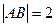 ,
,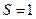 时,求直线
时,求直线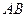 的方程.
的方程.
如图,直线
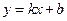 与椭圆
与椭圆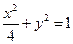 交于
交于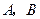 两点,记
两点,记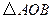 的面积为
的面积为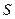 .
.(I)求在
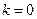 ,
,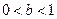 的条件下,
的条件下,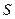 的最大值;
的最大值;(II)当
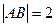 ,
,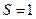 时,求直线
时,求直线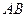 的方程.
的方程.(I)当且仅当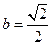 时,
时,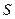 取到最大值
取到最大值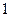 .
.
(II)直线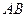 的方程是
的方程是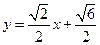 或
或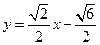 或
或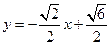 ,或
,或 .
.
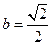 时,
时,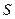 取到最大值
取到最大值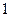 .
.(II)直线
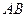 的方程是
的方程是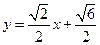 或
或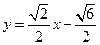 或
或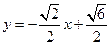 ,或
,或 .
.解:设点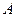 的坐标为
的坐标为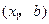 ,点
,点 的坐标为
的坐标为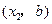 ,……1分
,……1分
由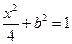 ,解得
,解得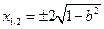 ,……3分
,……3分
所以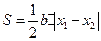
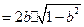
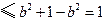 .…5分
.…5分
当且仅当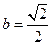 时,
时,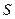 取到最大值
取到最大值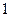 .…6分
.…6分
(Ⅱ)解:由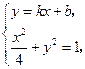 ……7分
……7分
得 ,
, ,①……8分
,①……8分
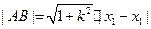
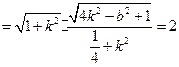 .② …9分
.② …9分
设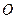 到
到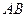 的距离为
的距离为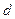 ,则
,则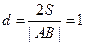 ,又因为
,又因为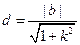 ,
,
所以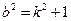 ,……10分
,……10分
代入②式并整理,得 ,解得
,解得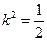 ,
,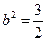 ,代入①式检验,
,代入①式检验,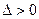 ,
,
故直线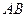 的方程是
的方程是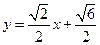 或
或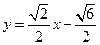 或
或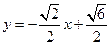 ,或
,或 .……14分(一条直线1分)
.……14分(一条直线1分)
 的坐标为
的坐标为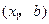 ,点
,点 的坐标为
的坐标为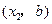 ,……1分
,……1分由
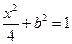 ,解得
,解得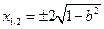 ,……3分
,……3分所以
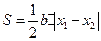
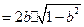
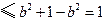 .…5分
.…5分当且仅当
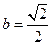 时,
时,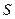 取到最大值
取到最大值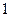 .…6分
.…6分(Ⅱ)解:由
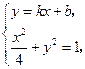 ……7分
……7分得
 ,
, ,①……8分
,①……8分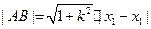
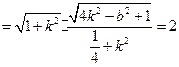 .② …9分
.② …9分 设
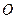 到
到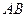 的距离为
的距离为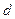 ,则
,则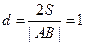 ,又因为
,又因为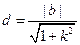 ,
,所以
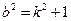 ,……10分
,……10分代入②式并整理,得
 ,解得
,解得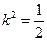 ,
,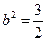 ,代入①式检验,
,代入①式检验,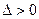 ,
,故直线
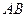 的方程是
的方程是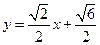 或
或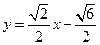 或
或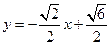 ,或
,或 .……14分(一条直线1分)
.……14分(一条直线1分)
练习册系列答案
相关题目
 的离心率
的离心率 ,且原点
,且原点 到直线
到直线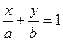 的距离为
的距离为 .
. 作直线与椭圆C交于
作直线与椭圆C交于 两点,求
两点,求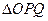 面积的最大值.
面积的最大值.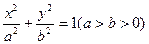 的左右焦点,M为椭圆上一点,MF2垂直于
的左右焦点,M为椭圆上一点,MF2垂直于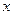 轴,椭圆下顶点和右顶点分别为A,B,且
轴,椭圆下顶点和右顶点分别为A,B,且
 ,求椭圆方程。
,求椭圆方程。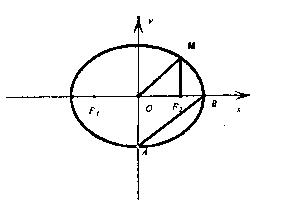
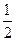 ,且椭圆E上一点到两个焦点距离之和为4;
,且椭圆E上一点到两个焦点距离之和为4;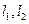 是过点P(0,2)且互相垂直的两条直线,
是过点P(0,2)且互相垂直的两条直线,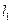 交E于A,B两点,
交E于A,B两点,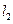 交E交C,D两点,AB,CD的中点分别为M,N。
交E交C,D两点,AB,CD的中点分别为M,N。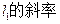 k的取值范围;
k的取值范围;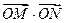 的取值范围。
的取值范围。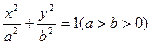 上一点,
上一点,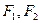 是椭圆的两焦点,且满足
是椭圆的两焦点,且满足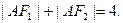
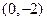 、
、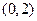 ,并且经过点
,并且经过点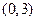 的椭圆方程是
的椭圆方程是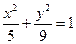 B.
B.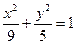 C.
C.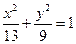 D.
D.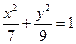
 的中心在原点,长轴在
的中心在原点,长轴在 轴上,离心率为
轴上,离心率为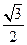 ,且
,且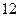 ,则椭圆
,则椭圆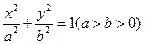 上任意一点,
上任意一点,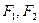 是其两个焦点,则
是其两个焦点,则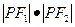 的取值范围是( )
的取值范围是( )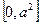
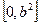
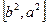

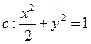 的两焦点为
的两焦点为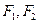 ,点
,点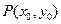 满足
满足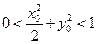 ,则|
,则|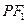 |+|
|+|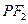 |的取值范围为_______,直线
|的取值范围为_______,直线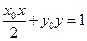 与椭圆C的公共点个数_____。
与椭圆C的公共点个数_____。