题目内容
(满分14分)已知A(1,1)是椭圆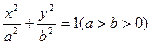 上一点,
上一点,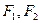 是椭圆的两焦点,且满足
是椭圆的两焦点,且满足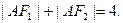
(1)求椭圆的两焦点坐标;
(2)设点C、D是椭圆上两点,直线AC、AD的倾斜角互补,试判断直线CD的斜率是否为定值?
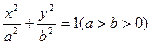 上一点,
上一点,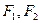 是椭圆的两焦点,且满足
是椭圆的两焦点,且满足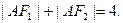
(1)求椭圆的两焦点坐标;
(2)设点C、D是椭圆上两点,直线AC、AD的倾斜角互补,试判断直线CD的斜率是否为定值?
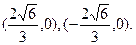
直线CD的斜率为定值1/3
解 (1)由椭圆定义知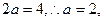 即椭圆方程为
即椭圆方程为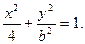
把(1,1)代入得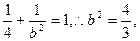 ,椭圆方程为
,椭圆方程为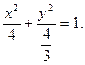
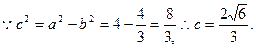
 故两焦点坐标为
故两焦点坐标为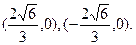
(2)由题意知,AC的倾斜角不为900,故设AC方程为: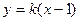 ,联立
,联立 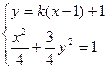 消去
消去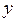 得
得 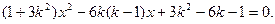
∵点A(1,1)、C在椭圆上,∴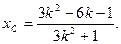
∵AC、AD直线倾斜角互补,∴AD的方程为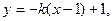 同理
同理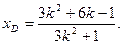
又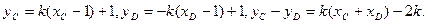
所以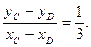 即直线CD的斜率为定值.
即直线CD的斜率为定值.
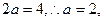 即椭圆方程为
即椭圆方程为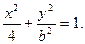
把(1,1)代入得
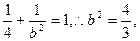 ,椭圆方程为
,椭圆方程为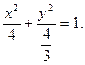
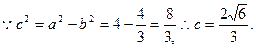
 故两焦点坐标为
故两焦点坐标为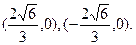
(2)由题意知,AC的倾斜角不为900,故设AC方程为:
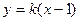 ,联立
,联立 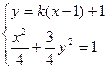 消去
消去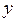 得
得 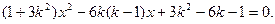
∵点A(1,1)、C在椭圆上,∴
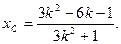
∵AC、AD直线倾斜角互补,∴AD的方程为
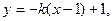 同理
同理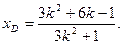
又
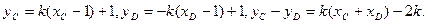
所以
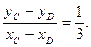 即直线CD的斜率为定值.
即直线CD的斜率为定值.
练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
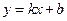 与椭圆
与椭圆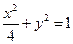 交于
交于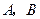 两点,记
两点,记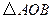 的面积为
的面积为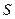 .
.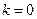 ,
,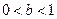 的条件下,
的条件下,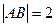 ,
,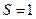 时,求直线
时,求直线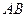 的方程.
的方程.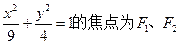 ,椭圆上动点P的坐标为
,椭圆上动点P的坐标为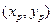 ,且
,且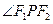 为钝角,求
为钝角,求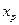 的取值范围。
的取值范围。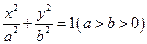 短轴的一个端点
短轴的一个端点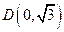 ,离心率
,离心率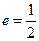 .过
.过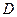 作直线
作直线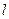 与椭圆交于另一点
与椭圆交于另一点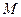 ,与
,与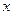 轴交于点
轴交于点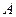 (不同于原点
(不同于原点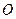 ),点
),点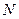 ,直线
,直线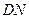 交
交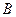 .
.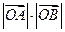 的值.
的值.
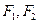 分别是椭圆
分别是椭圆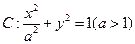 的左右焦点,直线
的左右焦点,直线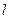 与C相交于A,B两点
与C相交于A,B两点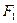 ,若
,若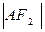 ,
,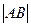 ,
,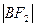 成等差数列,,求
成等差数列,,求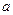 值
值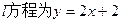 ,且
,且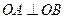 ,求
,求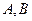 分别为椭圆
分别为椭圆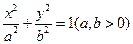 的左、右顶点,椭圆长半轴的长等于焦距,且
的左、右顶点,椭圆长半轴的长等于焦距,且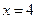 为它的右准线.
为它的右准线.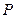 为右准线上不同于点(4,0)的任意一点,若直线
为右准线上不同于点(4,0)的任意一点,若直线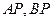 分别与椭圆相交于异于
分别与椭圆相交于异于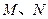 ,证明点
,证明点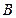 在以
在以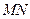 为直径的圆内.
为直径的圆内.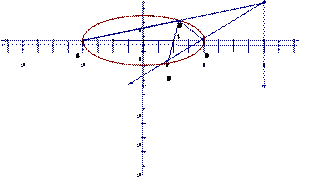
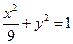 的两个焦点分别为
的两个焦点分别为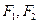 ,点
,点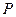 在椭圆上且
在椭圆上且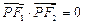 ,则Δ
,则Δ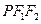 的面积是( )
的面积是( )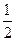
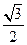
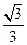
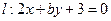 过椭圆
过椭圆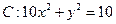 的一个焦点,则
的一个焦点,则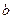 的值是( )
的值是( )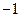
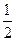
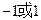
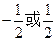
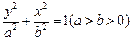 的上焦点为
的上焦点为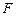 ,左、右顶点分别为
,左、右顶点分别为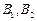 ,下顶点为
,下顶点为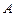 ,直线
,直线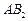 与直线
与直线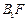 交于点
交于点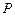 ,若
,若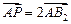 ,则椭圆的离心率为___________。
,则椭圆的离心率为___________。