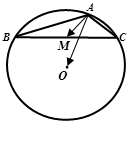题目内容
(本小题满分12分)已知圆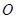 :
: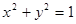 和定点
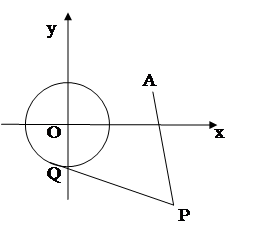
和定点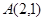 ,由圆外一点
,由圆外一点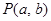 向圆
向圆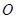 引切线
引切线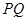 ,切点为
,切点为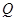 ,且满足
,且满足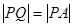 .
.
(1)求实数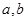 间满足的等量关系式;
间满足的等量关系式;
(2)求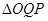 面积的最小值;
面积的最小值;
(3)求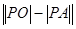 的最大值。
的最大值。
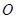 :
: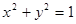 和定点
和定点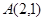 ,由圆外一点
,由圆外一点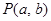 向圆
向圆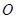 引切线
引切线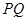 ,切点为
,切点为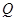 ,且满足
,且满足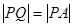 .
.
(1)求实数
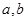 间满足的等量关系式;
间满足的等量关系式;(2)求
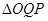 面积的最小值;
面积的最小值;(3)求
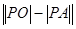 的最大值。
的最大值。(1)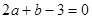 ;(2)
;(2)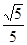 ;(3)
;(3)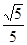
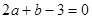 ;(2)
;(2)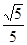 ;(3)
;(3)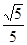
试题分析:(1)连结
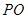 ,
,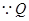 为切点,
为切点,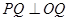 ,由勾股定理得
,由勾股定理得 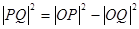
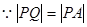 ,
,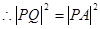 ,即
,即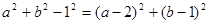
化简得
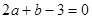
(2)
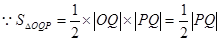 ,所以求
,所以求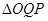 面积的最小值转化为求
面积的最小值转化为求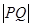 的最小值。
的最小值。法一:
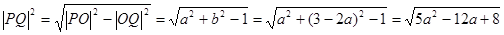
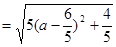 ,当
,当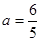 时,
时,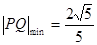
所以
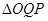 面积的最小值为
面积的最小值为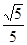
法二:点
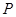 在直线
在直线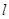 :
: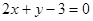 上
上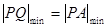
即求点
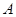 到直线
到直线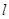 的距离
的距离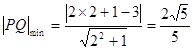
所以
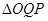 面积的最小值为
面积的最小值为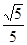
(3)设
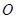 关于直线
关于直线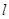 :
: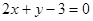 的对称点为
的对称点为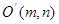
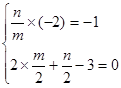 ,解得
,解得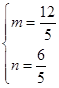
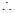
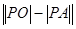
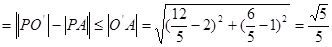
故
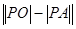 的最大值为
的最大值为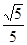
点评:对称问题的核心是点关于点的中心对称和点关于直线的轴对称,要充分利用转化的思想将问题转化为这两类对称中的一种加以处理

练习册系列答案
相关题目
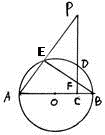
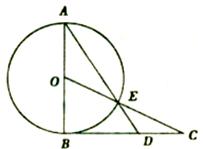
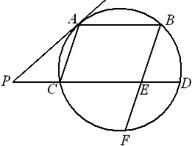
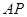 是
是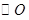 的切线,
的切线,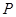 为切点,
为切点,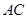 是
是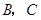 两点,圆心
两点,圆心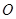 在
在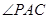 的内部,点
的内部,点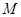 是
是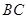 的中点.
的中点.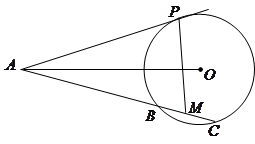
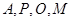 四点共圆;
四点共圆;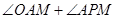 的大小.
的大小.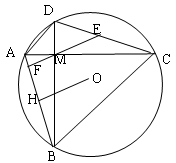
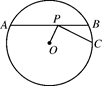
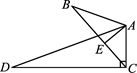
 为△
为△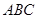 的外心,
的外心,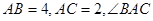 为钝角,
为钝角, 是边
是边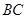 的中点,则
的中点,则 的值 ( ).
的值 ( ).