题目内容
设D是△ABC的BC边上一点,把△ACD沿AD折起,使C点所处的新位置C′在平面ABD上的射影H恰好在AB上.
(1)求证:直线C′D与平面ABD和平面AHC′所成的两个角之和不可能超过90°;
(2)若∠BAC=90°,二面角C′—AD—H为60°,求∠BAD的正切值.
???
(1)求证:直线C′D与平面ABD和平面AHC′所成的两个角之和不可能超过90°;
(2)若∠BAC=90°,二面角C′—AD—H为60°,求∠BAD的正切值.
???

(2)tanBAD=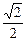
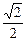
(1)证明:连结DH,∵C′H⊥平面ABD,∴∠C′DH为C′D与平面ABD所成
的角且平面C′HA⊥平面ABD,过D作DE⊥AB,垂足为E,则DE⊥平面C′HA.
故∠DC′E为C′D与平面C′HA所成的角
∵sinDC′E=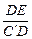 ≤
≤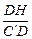 =sinDC′H
=sinDC′H
∴∠DC′E≤∠DC′H,
∴∠DC′E+∠C′DE≤∠DC′H+∠C′DE=90°
(2)解:作HG⊥AD,垂足为G,连结C′G,
则C′G⊥AD,故∠C′GH是二面角C′—AD—H的平面角
即∠C′GH=60°,计算得tanBAD=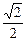
的角且平面C′HA⊥平面ABD,过D作DE⊥AB,垂足为E,则DE⊥平面C′HA.
故∠DC′E为C′D与平面C′HA所成的角
∵sinDC′E=
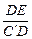 ≤
≤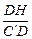 =sinDC′H
=sinDC′H∴∠DC′E≤∠DC′H,
∴∠DC′E+∠C′DE≤∠DC′H+∠C′DE=90°
(2)解:作HG⊥AD,垂足为G,连结C′G,
则C′G⊥AD,故∠C′GH是二面角C′—AD—H的平面角
即∠C′GH=60°,计算得tanBAD=
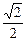

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
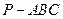 中,
中,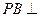 底面
底面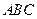 于
于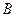 ,
,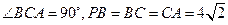 ,点
,点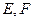 分别是
分别是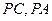 的中点,求二面角
的中点,求二面角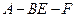 的余弦值.
的余弦值.
 ,空间中有一定点O,过点O有3条直线与a,b所成角都是60
,空间中有一定点O,过点O有3条直线与a,b所成角都是60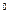 ,则
,则 的取值可能是( )
的取值可能是( )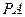 、
、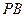 、
、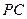 是从空间一点
是从空间一点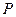 出发的三条射线,若
出发的三条射线,若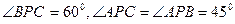 ,求二面角
,求二面角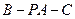 的大小.
的大小.

 中,
中,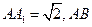
 为
为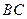 的中点
的中点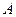 到面
到面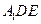 的距离;
的距离;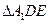 的重心为
的重心为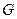 ,问是否存在实数
,问是否存在实数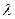 ,使
,使 且
且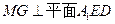 同时成立?若存
同时成立?若存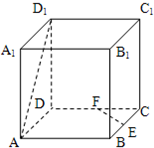
 中,
中, 与平面
与平面 所成的角的大小是( )
所成的角的大小是( )