题目内容
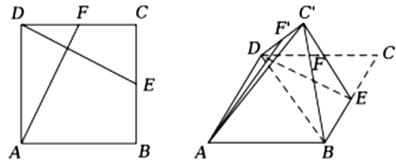
【题目】在正方形![]() 中,
中, ![]() 的中点为点
的中点为点![]() ,
, ![]() 的中点为点
的中点为点![]() ,沿
,沿![]() 将
将![]() 向上折起得到
向上折起得到![]() ,使得面
,使得面![]() 面
面![]() ,此时点
,此时点![]() 位于点
位于点![]() 处.
处.
(Ⅰ)证明: ![]() ;
;
(Ⅱ)求面![]() 与面
与面![]() 所成二面角的正弦值.
所成二面角的正弦值.
【答案】(Ⅰ)(Ⅱ)![]()
【解析】试题分析:(Ⅰ)利用折叠前后的不变量得到有关垂直关系,进而利用线面垂直的判定定理得到线面垂直,再利用线面垂直的性质得到线线垂直;(Ⅱ)同(Ⅰ)证明有关线面垂直和线线垂直,进而建立适当的空间直角坐标系,利用空间向量进行求解.
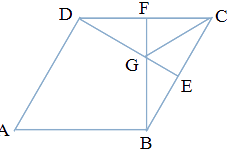
试题解析:(Ⅰ)证明:连接![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
, ![]() ,
,
如图所示,在正方形![]() 中,
中, ![]() 为
为![]() 中点,
中点, ![]() 为
为![]() 中点,所以
中点,所以![]() ;
;
由于![]() 为
为![]() 沿着
沿着![]() 翻折而来,从而
翻折而来,从而![]() ,所以
,所以![]() 面
面![]() ,
,
而![]() 在平面
在平面![]() 内,所以
内,所以![]() .
.

(Ⅱ)设![]() 中点为
中点为![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() . 同(Ⅰ)可证
. 同(Ⅰ)可证![]() ,从而面
,从而面![]() 面
面![]() ,所以
,所以![]() ;由
;由![]() 面
面![]() ,可得面
,可得面![]() 面
面![]() ,又因为面
,又因为面![]() 面
面![]() ,且面
,且面![]() 与面
与面![]() 相交于
相交于![]() ,所以
,所以![]() 面
面![]() .
.
设![]() 为原点,过点
为原点,过点![]() 作
作![]() 轴平行于
轴平行于![]() ,作
,作![]() 轴平行于
轴平行于![]() ,
, ![]() 为
为![]() 轴,如图所示,不妨设正方形
轴,如图所示,不妨设正方形![]() 边长为3,从而
边长为3,从而![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
又因为![]() ,所以
,所以![]() ,
, ![]() ,在直角
,在直角![]() 中,由勾股定理可得
中,由勾股定理可得![]() ,
,
所以![]() ,即
,即![]() ,所以可以求得面
,所以可以求得面![]() 的法向量
的法向量![]() 为
为![]() ,面
,面![]() 的法向量
的法向量![]() 为
为![]() ,所以可以得出法向量
,所以可以得出法向量![]() ,则所求二面角的正弦值为
,则所求二面角的正弦值为![]() .
.


练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
【题目】某书店销售刚刚上市的某知名品牌的高三数学单元卷,按事先拟定的价格进行5天试销,每种单价试销1天,得到如表数据:
单价x(元) | 18 | 19 | 20 | 21 | 22 |
销量y(册) | 61 | 56 | 50 | 48 | 45 |
(1)求试销5天的销量的方差和y对x的回归直线方程;
(2)预计今后的销售中,销量与单价服从(1)中的回归方程,已知每册单元卷的成本是14元,
为了获得最大利润,该单元卷的单价应定为多少元?