题目内容
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,抛物线上横坐标为
,抛物线上横坐标为![]() 的点到抛物线顶点的距离与该点到抛物线准线的距离相等。
的点到抛物线顶点的距离与该点到抛物线准线的距离相等。
(1)求抛物线![]() 的方程;
的方程;
(2)设直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,若
两点,若![]() ,求实数
,求实数![]() 的值。
的值。
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)将抛物线上点的横坐标![]() 代入方程
代入方程![]() ,求其纵坐标。因为抛物线上横坐标为
,求其纵坐标。因为抛物线上横坐标为![]() 的点到抛物线顶点的距离与其到准线的距离相等,用坐标表示距离相等,整理得
的点到抛物线顶点的距离与其到准线的距离相等,用坐标表示距离相等,整理得![]() ,进而求
,进而求![]() 。(2)设
。(2)设![]() ,
, ![]() ,直线与抛物线方程联立消x得
,直线与抛物线方程联立消x得![]() ,得出
,得出![]() 。由
。由![]() ,得
,得![]() ,即
,即![]() ,然后用坐标表示,可求
,然后用坐标表示,可求![]() 的值。
的值。
试题解析:(1)抛物线上横坐标为![]() 的点的坐标为
的点的坐标为![]() ,到抛物线顶点的距离的平方为
,到抛物线顶点的距离的平方为![]() ,
,
∵抛物线上横坐标为![]() 的点到抛物线顶点的距离与其到准线的距离相等,
的点到抛物线顶点的距离与其到准线的距离相等,
∴![]() ,
,
∴![]() ,
,
抛物线方程为: ![]() .
.
(2)由题意,直线![]() ,代入
,代入![]() 得,
得, ![]() ,
,
设![]() ,
, ![]() ,则
,则![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
可得: ![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得: ![]() .
.

练习册系列答案
相关题目
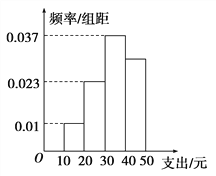
【题目】下表是某校高三一次月考5个班级的数学、物理的平均成绩:
班级 | 1 | 2 | 3 | 4 | 5 |
数学( | 111 | 113 | 119 | 125 | 127 |
物理( | 92 | 93 | 96 | 99 | 100 |
(Ⅰ)一般来说,学生的物理成绩与数学成绩具有线性相关关系,根据上表提供的数据,求两个变量![]() ,
, ![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)从以上5个班级中任选两个参加某项活动,设选出的两个班级中数学平均分在115分以上的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:  ,
, ![]()
【题目】某书店销售刚刚上市的某知名品牌的高三数学单元卷,按事先拟定的价格进行5天试销,每种单价试销1天,得到如下数据:
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
(1)求试销5天的销量的方差和![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(2)预计今后的销售中,销量与单价服从(1)中的回归方程,已知每册单元卷的成本是14元,为了获得最大利润,该单元卷的单价卷的单价应定为多少元?
(附: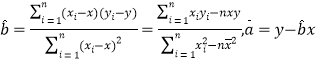 )
)