题目内容
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π,x∈R)在一个周期内的图象如图所示,则函数的解析式为 . 直线y= ![]() 与函数y=f(x)(x∈R)图象的所有交点的坐标为 .
与函数y=f(x)(x∈R)图象的所有交点的坐标为 . 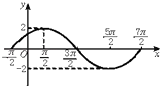
【答案】f(x)=2sin( ![]() ?x+
?x+ ![]() );(
);( ![]() ?+4kπ,
?+4kπ, ![]() )或(
)或( ![]() ?+4kπ,
?+4kπ, ![]() )(k∈Z)
)(k∈Z)
【解析】解:∵f(x)=Asin(ωx+φ)(A>0,ω>0,x∈R),
∴A=2,周期T= ![]() =
= ![]() ﹣(﹣
﹣(﹣ ![]() )=4π,
)=4π,
∴ω= ![]() .
.
∴f(x)=2sin( ![]() x+φ),
x+φ),
又f(﹣ ![]() )=2sin(
)=2sin( ![]() ×(﹣
×(﹣ ![]() )+φ)=0,
)+φ)=0,
∴φ﹣ ![]() =kπ,k∈Z,|φ|<π,
=kπ,k∈Z,|φ|<π,
∴φ= ![]() .
.
∴f(x)=2sin( ![]() x+
x+ ![]() ).
).
当f(x)= ![]() 时,即2sin(
时,即2sin( ![]() x+
x+ ![]() )=
)= ![]() ,可得sin(
,可得sin( ![]() x+
x+ ![]() )=
)= ![]() ,
,
∴ ![]() x+
x+ ![]() =
= ![]() +2kπ或
+2kπ或 ![]() x+
x+ ![]() =
= ![]() +2kπ(k∈Z),可得x=
+2kπ(k∈Z),可得x= ![]() +4kπ或
+4kπ或 ![]() +4kπ(k∈Z)
+4kπ(k∈Z)
由此可得,直线y= ![]() 与函数f(x)图象的所有交点的坐标为:(
与函数f(x)图象的所有交点的坐标为:( ![]() +4kπ,
+4kπ, ![]() )或(
)或( ![]() +4kπ,
+4kπ, ![]() )(k∈Z).
)(k∈Z).
故答案为:f(x)=2sin( ![]() x+
x+ ![]() ),(
),( ![]() +4kπ,
+4kπ, ![]() )或(
)或( ![]() +4kπ,
+4kπ, ![]() )(k∈Z).
)(k∈Z).
由函数f(x)=Asin(ωx+φ)的图象可知A=2,T=4π,从而可求ω,再由ω× ![]() +φ=
+φ= ![]() +2kπ可求得φ,从而可得答案.然后解方程2sin(
+2kπ可求得φ,从而可得答案.然后解方程2sin( ![]() x+
x+ ![]() )=
)= ![]() ,结合正弦函数的图象可得x=x=
,结合正弦函数的图象可得x=x= ![]() +4kπ或
+4kπ或 ![]() +4kπ(k∈Z),由此即可得到直线y=
+4kπ(k∈Z),由此即可得到直线y= ![]() 与函数f(x)图象的所有交点的坐标.
与函数f(x)图象的所有交点的坐标.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案【题目】某书店销售刚刚上市的某知名品牌的高三数学单元卷,按事先拟定的价格进行5天试销,每种单价试销1天,得到如下数据:
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
(1)求试销5天的销量的方差和![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(2)预计今后的销售中,销量与单价服从(1)中的回归方程,已知每册单元卷的成本是14元,为了获得最大利润,该单元卷的单价卷的单价应定为多少元?
(附: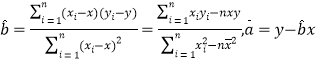 )
)
【题目】甲,乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于100为优品,大于等于90且小于100为合格品,小于90为次品,现随机抽取这两台车床生产的零件各100件进行检测,检测结果统计如下:
测试指标 |
|
|
|
|
|
机床甲 | 8 | 12 | 40 | 32 | 8 |
机床乙 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计甲机床、乙机床生产的零件为优品的概率;
(2)甲机床生产一件零件,若是优品可盈利160元,合格品可盈利100元,次品则亏损20元;假设甲机床某天生产50件零件,请估计甲机床该天的日利润(单位:元);
(3)从甲、乙机床生产的零件指标在![]() 内的零件中,采用分层抽样的方法抽取5件,从这5件中任选2件进行质量分析,求这2件都是乙机床生产的概率.
内的零件中,采用分层抽样的方法抽取5件,从这5件中任选2件进行质量分析,求这2件都是乙机床生产的概率.