题目内容
【题目】已知函数 ![]() ,
, ![]() .
.
(1)求函数 ![]() 的单调增区间;
的单调增区间;
(2)若 ![]() ,解不等式
,解不等式 ![]() ;
;
(3)若 ![]() ,且对任意
,且对任意 ![]() ,方程
,方程 ![]() 在
在 ![]() 总存在两不相等的实数根,求
总存在两不相等的实数根,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:∵ ![]() ,
,
∴ f(x)=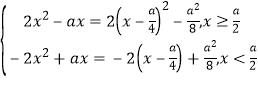
∴ ![]() :
: ![]() 的单调增区间为
的单调增区间为 ![]() ,
, ![]() ;
; ![]() :
: ![]() 的单调增区间为
的单调增区间为 ![]() ,
, ![]() ;
; ![]() :
: ![]() 的单调增区间为
的单调增区间为 ![]() ;
;
(2)解:∵ ![]() ,∴
,∴ ![]() 在
在 ![]() 单调递增,在
单调递增,在 ![]() 单调递减,在
单调递减,在 ![]() 单调递增,
单调递增,
若 ![]()
![]() :令
:令 ![]() 解得:
解得: ![]()
∴不等式的解为: ![]() ;若
;若 ![]()
![]() :令
:令 ![]() ,
,
解得: ![]() ,
, ![]() ,根据图象不等式的解为:
,根据图象不等式的解为: ![]() ,综上:
,综上: ![]() :不等式的解为
:不等式的解为 ![]() ;
; ![]() :不等式的解为
:不等式的解为 ![]() ;
;
(3)解: 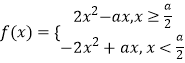 , ∵
, ∵ ![]() ,∴
,∴ ![]() 在
在 ![]() 单调递增,在
单调递增,在 ![]() 单调递减,在
单调递减,在 ![]() 单调递增,∴
单调递增,∴ ![]() ,
,
∴ ![]()
![]() 在
在 ![]() 单调递增,∴
单调递增,∴ ![]() ,
,![]() 在
在 ![]() 单调递减,在
单调递减,在 ![]() 单调递增,∴必须
单调递增,∴必须 ![]() ,
,
即 
![]()
![]() ,即实数
,即实数 ![]() 的取值范围是
的取值范围是 ![]() .
.
【解析】(1)根据绝对值的应用,结合函数的单调性进行判断.
(2)根据一元二次不等式的解法进行求解即可.
(3)根据函数单调性的性质,结合函数与方程的关系进行求解即可. 判断函数的单调性,有四种方法:定义法;导数法;函数图象法;基本函数的单调性的应用;复合函数遵循“同增异减”;证明方法有定义法;导数法.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减).
在这个区间单调递减).

练习册系列答案
相关题目