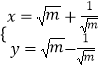ĢāÄæÄŚČŻ
”¾ĢāÄæ”æijŅūĮĻÉś²śĘóŅµĪŖĮĖÕ¼ÓŠøü¶ąµÄŹŠ³”·Ż¶ī£¬ÄāŌŚ2017Äź¶Č½ųŠŠŅ»ĻµĮŠ“ŁĻś»ī¶Æ£¬¾¹żŹŠ³”µ÷²éŗĶ²āĖć£¬ŅūĮĻµÄÄźĻśŹŪĮæxĶņ¼žÓėÄź“ŁĻś·ŃtĶņŌŖ¼äĀś×ć ![]() .ŅŃÖŖ2017ğɜ²śŅūĮĻµÄÉč±øÕŪ¾É£¬Ī¬ŠŽµČ¹Ģ¶Ø·ŃÓĆĪŖ3ĶņŌŖ£¬ĆæÉś²ś1Ķņ¼žŅūĮĻŠčŌŁĶ¶Čė32ĶņŌŖµÄÉś²ś·ŃÓĆ£¬Čō½«Ć漞ŅūĮĻµÄŹŪ¼Ū¶ØĪŖĘäÉś²ś³É±¾µÄ150%ÓėĘ½¾łĆ漞“ŁĻś·ŃµÄŅ»°ėÖ®ŗĶ£¬ŌņøĆğɜ²śµÄŅūĮĻÕżŗĆÄÜĻśŹŪĶź£®
.ŅŃÖŖ2017ğɜ²śŅūĮĻµÄÉč±øÕŪ¾É£¬Ī¬ŠŽµČ¹Ģ¶Ø·ŃÓĆĪŖ3ĶņŌŖ£¬ĆæÉś²ś1Ķņ¼žŅūĮĻŠčŌŁĶ¶Čė32ĶņŌŖµÄÉś²ś·ŃÓĆ£¬Čō½«Ć漞ŅūĮĻµÄŹŪ¼Ū¶ØĪŖĘäÉś²ś³É±¾µÄ150%ÓėĘ½¾łĆ漞“ŁĻś·ŃµÄŅ»°ėÖ®ŗĶ£¬ŌņøĆğɜ²śµÄŅūĮĻÕżŗĆÄÜĻśŹŪĶź£®
£Ø1£©½«2017ÄźµÄĄūČóy(ĶņŌŖ)±ķŹ¾ĪŖ“ŁĻś·Ńt(ĶņŌŖ)µÄŗÆŹż£»
£Ø2£©øĆĘóŅµ2017ÄźµÄ“ŁĻś·ŃĶ¶Čė¶ąÉŁĶņŌŖŹ±£¬ĘóŅµµÄÄźĄūČó×ī“ó£æ
(×¢£ŗĄūČó£½ĻśŹŪŹÕČė£Éś²ś³É±¾£“ŁĻś·Ń£¬Éś²ś³É±¾£½¹Ģ¶Ø·ŃÓĆ£«Éś²ś·ŃÓĆ)
”¾“š°ø”æ
£Ø1£©½ā£ŗµ±ÄźĻśĮæĪŖxĶņ¼žŹ±£¬³É±¾ĪŖ3£«32x(ĶņŌŖ)£®
ŅūĮĻµÄŹŪ¼ŪĪŖ ![]() ”Į150%£«
”Į150%£« ![]() ”Į
”Į ![]() (ĶņŌŖ/Ķņ¼ž)£¬
(ĶņŌŖ/Ķņ¼ž)£¬
ĖłŅŌÄźĄūČóy£½ ![]() x£(3£«32x£«t)(ĶņŌŖ)£¬
x£(3£«32x£«t)(ĶņŌŖ)£¬
°Ńx£½ ![]() “śČėÕūĄķµĆµ½y£½
“śČėÕūĄķµĆµ½y£½ ![]() £¬ĘäÖŠt”Ż0.
£¬ĘäÖŠt”Ż0.
£Ø2£©½ā£ŗÓÉ(1)ÖŖy£½ ![]() £½
£½ ![]() £½50£
£½50£ ![]() ”Ü50£2
”Ü50£2 ![]() £½42(ĶņŌŖ)£¬
£½42(ĶņŌŖ)£¬
µ±ĒŅ½öµ± ![]() £½
£½ ![]() £¬¼“t£½7Ź±£¬ymax£½42.
£¬¼“t£½7Ź±£¬ymax£½42.
ĖłŅŌøĆĘóŅµ2017ÄźµÄ“ŁĻś·ŃĶ¶Čė7ĶņŌŖŹ±£¬ĘóŅµµÄÄźĄūČó×ī“óĪŖ42ĶņŌŖ£®
”¾½āĪö”æ£Ø1£©Č·¶ØŅūĮĻµÄŹŪ¼Ū£¬¼“æÉĶعżx±ķŹ¾³öÄźĄūČóy£¬»Æ¼ņ“śČėÕūĄķ¼“æÉĒó³öyĶņŌŖ±ķŹ¾ĪŖ“ŁĻś·ŃtĶņŌŖµÄŗÆŹż£»
£Ø2£©øł¾ŻŅŃÖŖ“śČė£Ø1£©µÄŗÆŹż£¬·Ö±š½ųŠŠ»Æ¼ņ£¬ĄūÓĆ¹ŲÓŚtµÄ·½³Ģ±ŲŠėÓŠĮ½Õżøł½ØĮ¢¹ŲĻµŹ½£¬æÉĒó³ö×īÖµ£¬¼““ŁĻś·ŃĶ¶Čė¶ąÉŁĶņŌŖŹ±£¬ĘóŅµµÄÄźĄūČó×ī“ó£®